基本概念
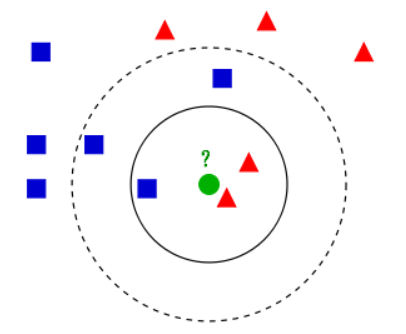
k 近邻算法是一种经典且简单的机器学习算法之一,用于分类和回归。在本文只探讨分类问题中的 k 近邻法。
k 近邻算法是一种少数服从多数的思想。给定一个训练数据集,数据集中的每一条数据都由一个特征向量表出如$(x_1, x_2…)$,每一条数据对应一个类别即标签。
我们输入一个新数据的向量到该数据集中,我们找到与该实例最邻近 的 $K$ 个实例,这$K$个实例中的多数属于某个类, 那么我们就把该输入实例分类到这个类中。(注:需要保证样本特征向量的长度一致)。
数据样本之间的距离可以用欧式距离和曼哈顿距离 来衡量。
算法实现 欧氏距离计算
1 2 3 4 5 6 7 8 9 def L (x, y, p=2 ) : if len(x) == len(y) and len(x) > 1 : sum = 0 for i in range(len(x)): sum += math.pow(abs(x[i] - y[i]), p) return math.pow(sum, 1 /p) else : return 0
Knn算法实现
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 class KNN : def __init__ (self, X_train, y_train, n_neighbors=3 , p=2 ) : """ parameter: n_neighbors 临近点个数 parameter: p 距离度量 """ self.n = n_neighbors self.p = p self.X_train = X_train self.y_train = y_train def predict (self, X) : knn_list = [] for i in range(self.n): dist = np.linalg.norm(X - self.X_train[i], ord=self.p) knn_list.append((dist, self.y_train[i])) for i in range(self.n, len(self.X_train)): max_index = knn_list.index(max(knn_list, key=lambda x: x[0 ])) dist = np.linalg.norm(X - self.X_train[i], ord=self.p) if knn_list[max_index][0 ] > dist: knn_list[max_index] = (dist, self.y_train[i]) knn = [k[-1 ] for k in knn_list] count_pairs = Counter(knn) max_count = sorted(count_pairs, key=lambda x:x)[-1 ] return max_count def score (self, X_test, y_test) : right_count = 0 n = 10 for X, y in zip(X_test, y_test): label = self.predict(X) if label == y: right_count += 1 return right_count / len(X_test)
Last updated: 2019-03-08 14:32:03
Thanks for your reading :) | URL
https://joshuaqyh.github.io/2018/12/24/机器学习-K近邻算法/