基本原理

基本概念

最简单的支持向量机是一个二分类的分类器。分类思想是给定一组包含正负样本的集合，然后找到一个超平面（可以是一维或者多维），来对正负样本进行分割。

该方法对于解决小样本，非线性，及高维模式识别中表现出许多的优势。

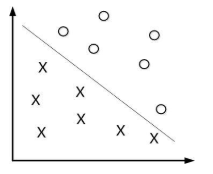
以下图的直线就是概念中的超平面，将样本划分为两个类别。在解决实际的多分类问题中可以转化为多个二分类问题。

其中的超平面方程由以下线性方程来描述。

​ $$g(x) = w^Tx + b = 0$$

其中$x$为样本的特征向量，$w^T$ 代表平面的法向量，而 $b$ 代表超平面的偏移量。

假设输入样本为 $x_0$，使得 $g(x_0) > 0$ 的样本为正样本，反之为负样本，正负标签记为 ${+1, -1} $。

函数间隔

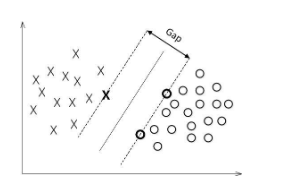
函数的间隔指的是正负样本点中到超平面的最近距离。对数据点进行分类，当超平面离数据点的间隔越大，分类的确信度越高。故当多个超平面的分类准确率一致时，我们要着重考虑最大间隔的分类器。

所以支持向量机的最终目标就是找到一个最大间隔的分类器。可以理解为一个约束优化问题，用以下式子来表示。

$$max \, \frac{r^}{||w||} \ subject\, to \, y_i (w^Tx_i + b ) \ge r^ $$

其中 $r^*$为函数间隔。

① 该方程并非凸函数求解，所以将方程转化为凸函数。转化为以下约束优化问题。

$$min \, \frac{1}{||w||} \ subject \,to\, y_i(w^Tx_i + b) \geq r*$$

转为凸函数以后，使用拉格朗日乘子法和KTT条件求解对偶问题。

②用拉格朗日乘子法和KKT条件求解最优值：

$$\min\ \frac{1}{2}||w||^2$$

$$s.t.\ -y_i(w^Tx_i+b)+1\leq 0,\ i=1,2,..,m$$

整合成：

$$L(w, b, \alpha) = \frac{1}{2}||w||^2+\sum^m_{i=1}\alpha_i(-y_i(w^Tx_i+b)+1)$$

推导：$\min\ f(x)=\min \max\ L(w, b, \alpha)\geq \max \min\ L(w, b, \alpha)$

根据KKT条件：

$$\frac{\partial }{\partial w}L(w, b, \alpha)=w-\sum\alpha_iy_ix_i=0,\ w=\sum\alpha_iy_ix_i$$

$$\frac{\partial }{\partial b}L(w, b, \alpha)=\sum\alpha_iy_i=0$$

带入$ L(w, b, \alpha)$

$\min\ L(w, b, \alpha)=\frac{1}{2}||w||^2+\sum^m_{i=1}\alpha_i(-y_i(w^Tx_i+b)+1)$

$\qquad\qquad\qquad=\frac{1}{2}w^Tw-\sum^m_{i=1}\alpha_iy_iw^Tx_i-b\sum^m_{i=1}\alpha_iy_i+\sum^m_{i=1}\alpha_i$

$\qquad\qquad\qquad=\frac{1}{2}w^T\sum\alpha_iy_ix_i-\sum^m_{i=1}\alpha_iy_iw^Tx_i+\sum^m_{i=1}\alpha_i$

$\qquad\qquad\qquad=\sum^m_{i=1}\alpha_i-\frac{1}{2}\sum^m_{i=1}\alpha_iy_iw^Tx_i$

$\qquad\qquad\qquad=\sum^m_{i=1}\alpha_i-\frac{1}{2}\sum^m_{i,j=1}\alpha_i\alpha_jy_iy_j(x_ix_j)$

再把max问题转成min问题：

$\max\ \sum^m_{i=1}\alpha_i-\frac{1}{2}\sum^m_{i,j=1}\alpha_i\alpha_jy_iy_j(x_ix_j)=\min \frac{1}{2}\sum^m_{i,j=1}\alpha_i\alpha_jy_iy_j(x_ix_j)-\sum^m_{i=1}\alpha_i$

$s.t.\ \sum^m_{i=1}\alpha_iy_i=0,$

$ \alpha_i \geq 0,i=1,2,…,m$

以上为SVM对偶问题的对偶形式

kernel

在低维空间计算获得高维空间的计算结果，也就是说计算结果满足高维（满足高维，才能说明高维下线性可分）。

soft margin & slack variable

引入松弛变量$\xi\geq0$，对应数据点允许偏离的functional margin 的量。

目标函数：$\min\ \frac{1}{2}||w||^2+C\sum\xi_i\qquad s.t.\ y_i(w^Tx_i+b)\geq1-\xi_i$

对偶问题：

$$\max\ \sum^m_{i=1}\alpha_i-\frac{1}{2}\sum^m_{i,j=1}\alpha_i\alpha_jy_iy_j(x_ix_j)=\min \frac{1}{2}\sum^m_{i,j=1}\alpha_i\alpha_jy_iy_j(x_ix_j)-\sum^m_{i=1}\alpha_i$$

$$s.t.\ C\geq\alpha_i \geq 0,i=1,2,…,m\quad \sum^m_{i=1}\alpha_iy_i=0,$$

Sequential Minimal Optimization

首先定义特征到结果的输出函数：$u=w^Tx+b$.

因为$w=\sum\alpha_iy_ix_i$

有$u=\sum y_i\alpha_iK(x_i, x)-b$

$\max \sum^m_{i=1}\alpha_i-\frac{1}{2}\sum^m_{i=1}\sum^m_{j=1}\alpha_i\alpha_jy_iy_j<\phi(x_i)^T,\phi(x_j)>$

$s.t.\ \sum^m_{i=1}\alpha_iy_i=0,$

$ \alpha_i \geq 0,i=1,2,…,m$

参考资料：

[1] :Lagrange Multiplier and KKT

[2] :推导SVM

[3] :机器学习算法实践-支持向量机(SVM)算法原理

[4] :Python实现SVM

python 实现

以下是利用sklearn的一个简单实现。

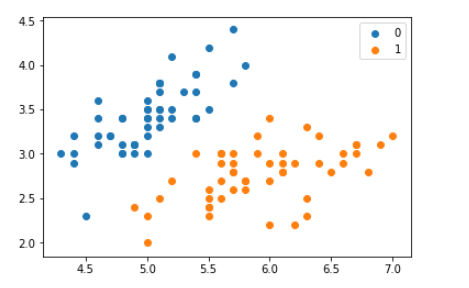
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
import numpy as np
import pandas as pd
from sklearn.datasets import load_iris
from sklearn.model_selection import  train_test_split
import matplotlib.pyplot as plt
%matplotlib inline

# data
def create_data():
    iris = load_iris()
    df = pd.DataFrame(iris.data, columns=iris.feature_names)
    df['label'] = iris.target
    df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']
    data = np.array(df.iloc[:100, [0, 1, -1]])
    for i in range(len(data)):
        if data[i,-1] == 0:
            data[i,-1] = -1
    # print(data)
    return data[:,:2], data[:,-1]

## 生成数据集并显示 
X, y = create_data()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25)
plt.scatter(X[:50,0],X[:50,1], label='0')
plt.scatter(X[50:,0],X[50:,1], label='1')
plt.legend()

数据集如上。

SVM实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
class SVM:
    def __init__(self, max_iter=100, kernel='linear'):
        self.max_iter = max_iter
        self._kernel = kernel
    
    def init_args(self, features, labels):
        self.m, self.n = features.shape
        self.X = features
        self.Y = labels
        self.b = 0.0
        
        # 将Ei保存在一个列表里
        self.alpha = np.ones(self.m)
        self.E = [self._E(i) for i in range(self.m)]
        # 松弛变量
        self.C = 1.0
        
    def _KKT(self, i):
        y_g = self._g(i)*self.Y[i]
        if self.alpha[i] == 0:
            return y_g >= 1
        elif 0 < self.alpha[i] < self.C:
            return y_g == 1
        else:
            return y_g <= 1
    
    # g(x)预测值，输入xi（X[i]）
    def _g(self, i):
        r = self.b
        for j in range(self.m):
            r += self.alpha[j]*self.Y[j]*self.kernel(self.X[i], self.X[j])
        return r
    
    # 核函数
    def kernel(self, x1, x2):
        if self._kernel == 'linear':
            return sum([x1[k]*x2[k] for k in range(self.n)])
        elif self._kernel == 'poly':
            return (sum([x1[k]*x2[k] for k in range(self.n)]) + 1)**2
    
        return 0
    
    # E（x）为g(x)对输入x的预测值和y的差
    def _E(self, i):
        return self._g(i) - self.Y[i]
    
    def _init_alpha(self):
        # 外层循环首先遍历所有满足0<a<C的样本点，检验是否满足KKT
        index_list = [i for i in range(self.m) if 0 < self.alpha[i] < self.C]
        # 否则遍历整个训练集
        non_satisfy_list = [i for i in range(self.m) if i not in index_list]
        index_list.extend(non_satisfy_list)
        
        for i in index_list:
            if self._KKT(i):
                continue
            
            E1 = self.E[i]
            # 如果E2是+，选择最小的；如果E2是负的，选择最大的
            if E1 >= 0:
                j = min(range(self.m), key=lambda x: self.E[x])
            else:
                j = max(range(self.m), key=lambda x: self.E[x])
            return i, j
        
    def _compare(self, _alpha, L, H):
        if _alpha > H:
            return H
        elif _alpha < L:
            return L
        else:
            return _alpha      
    
    def fit(self, features, labels):
        self.init_args(features, labels)
        
        for t in range(self.max_iter):
            # train
            i1, i2 = self._init_alpha()
            
            # 边界
            if self.Y[i1] == self.Y[i2]:
                L = max(0, self.alpha[i1]+self.alpha[i2]-self.C)
                H = min(self.C, self.alpha[i1]+self.alpha[i2])
            else:
                L = max(0, self.alpha[i2]-self.alpha[i1])
                H = min(self.C, self.C+self.alpha[i2]-self.alpha[i1])
                
            E1 = self.E[i1]
            E2 = self.E[i2]
            # eta=K11+K22-2K12
            eta = self.kernel(self.X[i1], self.X[i1]) + self.kernel(self.X[i2], self.X[i2]) - 2*self.kernel(self.X[i1], self.X[i2])
            if eta <= 0:
                # print('eta <= 0')
                continue
                
            alpha2_new_unc = self.alpha[i2] + self.Y[i2] * (E2 - E1) / eta
            alpha2_new = self._compare(alpha2_new_unc, L, H)
            
            alpha1_new = self.alpha[i1] + self.Y[i1] * self.Y[i2] * (self.alpha[i2] - alpha2_new)
            
            b1_new = -E1 - self.Y[i1] * self.kernel(self.X[i1], self.X[i1]) * (alpha1_new-self.alpha[i1]) - self.Y[i2] * self.kernel(self.X[i2], self.X[i1]) * (alpha2_new-self.alpha[i2])+ self.b 
            b2_new = -E2 - self.Y[i1] * self.kernel(self.X[i1], self.X[i2]) * (alpha1_new-self.alpha[i1]) - self.Y[i2] * self.kernel(self.X[i2], self.X[i2]) * (alpha2_new-self.alpha[i2])+ self.b 
            
            if 0 < alpha1_new < self.C:
                b_new = b1_new
            elif 0 < alpha2_new < self.C:
                b_new = b2_new
            else:
                # 选择中点
                b_new = (b1_new + b2_new) / 2
                
            # 更新参数
            self.alpha[i1] = alpha1_new
            self.alpha[i2] = alpha2_new
            self.b = b_new
            
            self.E[i1] = self._E(i1)
            self.E[i2] = self._E(i2)
        return 'train done!'
            
    def predict(self, data):
        r = self.b
        for i in range(self.m):
            r += self.alpha[i] * self.Y[i] * self.kernel(data, self.X[i])
            
        return 1 if r > 0 else -1
    
    def score(self, X_test, y_test):
        right_count = 0
        for i in range(len(X_test)):
            result = self.predict(X_test[i])
            if result == y_test[i]:
                right_count += 1
        return right_count / len(X_test)
    
    def _weight(self):
        # linear model
        yx = self.Y.reshape(-1, 1)*self.X
        self.w = np.dot(yx.T, self.alpha)
        return self.w