向量与线性方程组
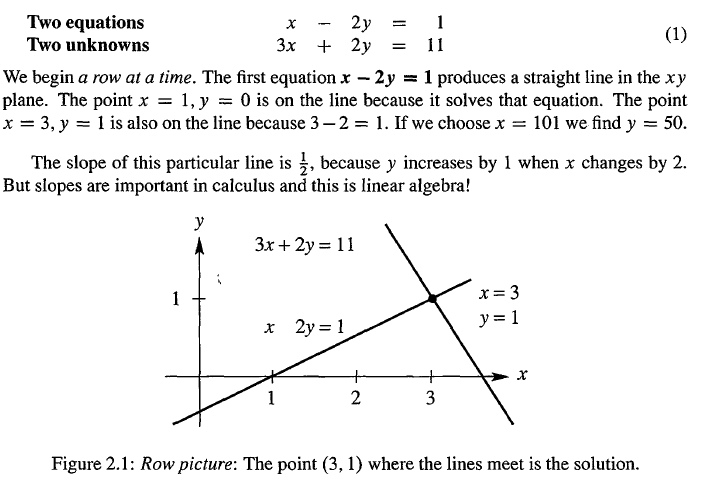
行图像
在二维平面中,行图像就是每一道方程所对应的线相交与一点。(更高维情况,就是低一维的对象相交得到低两维的对象)。点的坐标就是线性方程组的解。
列图像
列图像就是将线性方程组写成线性组合的形式,在平面内进行几何向量的运算。
- 线性组合中的列向量就是方程中每一个未知数所有系数构成的向量
- 线性组合中的系数就是方程组的未知数
- 线性组合中的结果就是方程组的解构成的列向量

矩阵-向量乘法


以上内容都是基于二阶线性方程组和二维平面内进行的,在高维的情况下可直接推广。这里不做赘述。
Elimination 消去
通常在求解一个线性方程组,无法直接构造适用的线性系统A,需要对原方程组进行一定的变化,这些变化方法统称为 消去,最终得到一个上三角矩阵 A。(主对角线以下都是0的方阵称为上三角矩阵)
上三角矩阵具备以下性质:
2、上三角矩阵乘以系数后也是上三角矩阵;
3、上三角矩阵间的加减法和乘法运算的结果仍是上三角矩阵;
4、上三角矩阵的逆矩阵也仍然是上三角矩阵。
5、这些事实说明:所有上三角矩阵的集合以及相应的运算构成一个方形矩阵集合的一个子代数。
一般需要对原方程组进行 行交换,乘以系数,或者方程相减等操作,从而得到化简后的上三角矩阵。
Matrix Multiplication 矩阵乘法
定义
矩阵乘法的规则(考虑3列的情形):
$$AB = A [b_1 \, b_2 b_3] = [Ab_1\, Ab_2\, Ab_3] \tag{1}$$
A 为 m × n 的矩阵,B为 n × o 的矩阵,乘法结果就是 m × o 的矩阵。
A B 矩阵需要满足上述的行列数目规则, A的列数等于B的行数。
乘法性质
- 结合律成立
- 交换律不成立
常见操作
利用一些置换矩阵来完成矩阵操作:
- 行交换

- 消除某些行
增广矩阵
对于 Ax = b,其增广矩阵为 [ A b ]
矩阵运算法则
矩阵相乘

运算律

块矩阵和块乘法

逆矩阵
定义

但是不是所有矩阵都有逆矩阵!
若矩阵可逆,那么该矩阵和逆矩阵相乘的结果就是单位矩阵!
引理
关于逆矩阵有以下几个引理,常用的有 Note5.


矩阵乘法的逆矩阵
如果矩阵 A,B都是可逆矩阵,那么 AB 的逆矩阵就是
$$(AB)^{-1} = B^{-1}A^{-1} \tag{2}$$

$$(ABC\dots Z)^{-1} = Z^{-1}\dots C^{-1}B^{-1}A^{-1} \tag{3}$$
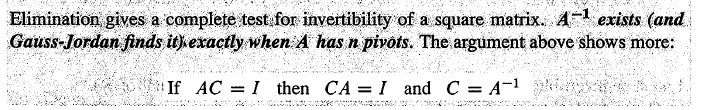
Calculating $A^{-1}$ by Gauss-Jordan Elimination
考虑三列的情形:
$$AA^{-1} = A[x_1\, x_2\, x_3 ] = [e_1 \, e_2 \, e_3] = I$$
处理成近似 Ax = b的情况。
构造增广矩阵 $[A \, e_1 \, e_2 \,e_3] $ , 利用消去运算,将增广矩阵改造成 $[I \, A^{-1}]$,从而得到 $A^{-1}$。
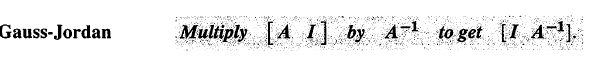
A = LU 矩阵因式分解
概述
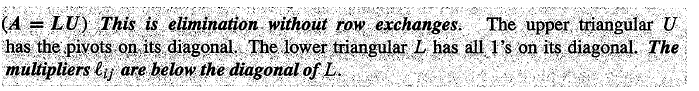
给定一个A矩阵,要找出一个下三角矩阵L和一个上三角矩阵U,使得 A = LU
L和U的好处就是将稠密的A矩阵转为两个稀疏矩阵L、U,减低计算复杂度,提升计算速度。
计算 L和U
对于一个式子 A = LU,各矩阵解释如下:
- A 为一个初始矩阵,待分解。
- U 为 A矩阵经过矩阵消元得到的上三角矩阵。
- L 为一个下三角矩阵,可以根据行变换的倍数和行,在单元矩阵上填充非0数。
转置
定义

性质

对称矩阵
- 定义

- 对称矩阵的生成方法 $R^T R $
给定任意的一个矩阵 R,我们可以使用 其转置$R^T$与R相乘,得到一个正方形的对称矩阵。

- 对称矩阵的分解性质 $LDL^T$
对于一个矩阵 A,我们考虑其因式分解 A = LDU。如果A为对称矩阵,那么U = $L^T$ 。
置换矩阵

置换就是对原矩阵进行变换,包括系数变换,行交换。