向量空间
向量空间定义
一个空间 $R^n$ 包含着 所有的 n 维的列向量 v,那么该空间就是向量空间。

还有三种特殊的向量空间 M、F、Z。
子空间

对于子空间的任意两个 v w向量(包括 零向量),满足 v + w 存在子空间中,cv 也在子空间中(可推导得到 v w 的线性组合都在子空间中)。 此时子空间记为 span{v,w}
即:
包含零向量
向量加法封闭
向量乘法封闭
列空间
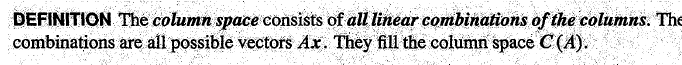
对于 Ax = b,我们探讨 A的列空间。
列空间就是矩阵(A)中所有列向量的所有可能线性组合(Ax)的结果 (b),这些结果构成矩阵 (A)列空间C(A)。
对于一个 系统 Ax = b,若是可解的,当且仅当b位于A的列空间之中。
A的零空间:解决 Ax = 0
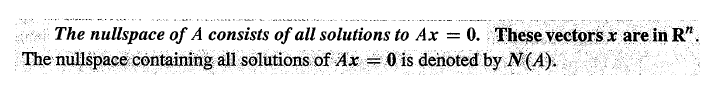
零空间内部的向量x,经过矩阵A变换,得到的解为0向量。
例子:

给出一个矩阵A的零空间的特殊解,该零空间是特殊解的所有可能的线性组合的结果。

行阶梯矩阵

秩和行简化的形式
秩定义
矩阵的秩用来描述矩阵的大小,矩阵 A 的秩等于 rank A = 矩阵主元的个数,同时也是矩阵列空间的维数,此外我们也可以用秩来描述矩阵的独立行的个数。
主元 自由变量
主元(pivot)的含义就是在简化后矩阵的每一行第一个非0值就是主元.。
自由变量的含义就是就是可以任取的变量,位置处于非主元列的非主元元素。
主元列 自由列
主元所在的列叫做主元列,非主元列称为自由列。
自由列可以由未化简之前的主元列进行线性组合得到,线性组合的结果就是特殊解。

从自由列和自由变量可以发现特殊解。

零空间的生成集
我们可以利用自由变量和主元来求出零空间的一个生成集。主元可以用其他自由变量线性组合得到,代入原式可以得到一组自由变量作为权的向量组合。

秩为1的矩阵

Ax = b的完全解
之前求解Ax = 0 就是 Ax = b 的一个特殊情况(b = 0 向量)
求解Ax = b,我们先设计一个增广矩阵[ A b ],对其进行行简化。
求出一个通解和一个特殊解,然后 完全解 = 通解 + 特殊解

满列秩
满列秩矩阵就是主元的个数等于矩阵的行数的矩阵,所有列都具有主元。其性质如下:

满行秩
满行秩矩阵的每一行都存在主元。

对于一个 m × n 矩阵,其秩 r 与 m n 之间存在四种可能的情况:

独立性 基 和维度

线性独立
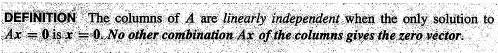
对于一个矩阵来说,线性独立意味着 Ax = 0的解只有 x = 0。零空间中只有 x = 0.
对于一组向量来说,若都处于同一平面的话,则成向量线性依赖,若不在同一平面内,则这组向量线性独立。(一组向量也可以看成一个矩阵)
公式化结果如下:

展开成子空间
一组向量扩展成一个空间的条件就是该组向量的线性组合能够填充整个空间。


矩阵A的行空间是$A^T$ 的列空间。
向量基
对于一个空间$R^n$,可存在多组向量基。每一组向量基可展开填满空间$R^n$。
每一组基有n个基向量,这些基向量线性独立(即不在同一平面内)并且展开可填满整个$R^n$空间。
如果基向量相互垂直(正交),那么称为标准正交基。
此时空间的维度就等于每一组基中向量的个数。
矩阵空间和函数空间的基

四个子空间的维度
