贝叶斯原理
基本概念
贝叶斯原理其实是在求解一个逆向概率的问题。
我们用一个题目来体会下:假设有一种病叫做“贝叶死”,它的发病率是万分之一,即 10000 人中会有 1 个人得病。现有一种测试可以检验一个人是否得病的准确率是 99.9%,它的误报率是 0.1%,那么现在的问题是,如果一个人被查出来患有“叶贝死”,实际上患有的可能性有多大?
你可能会想说,既然查出患有“贝叶死”的准确率是 99.9%,那是不是实际上患“贝叶死”的概率也是 99.9% 呢?实际上不是的。你自己想想,在 10000 个人中,还存在 0.1% 的误查的情况,也就是 10 个人没有患病但是被诊断成阳性。当然 10000 个人中,也确实存在一个患有贝叶死的人,他有 99.9% 的概率被检查出来。所以你可以粗算下,患病的这个人实际上是这 11 个人里面的一员,即实际患病比例是 1/11≈9%。
以上涉及了贝叶斯原理的几个核心概念:
- 先验概率:通过经验来判断事情发生的概率,比如说“贝叶死”的发病率是万分之一,就是先验概率。再比如南方的梅雨季是 6-7 月,就是通过往年的气候总结出来的经验,这个时候下雨的概率就比其他时间高出很多。
- 后验概率:后验概率就是发生结果之后,推测原因的概率。比如说某人查出来了患有“贝叶死”,那么患病的原因可能是 A、B 或 C。患有“贝叶死”是因为原因 A 的概率就是后验概率。它是属于条件概率的一种。
- 条件概率:事件 A 在另外一个事件 B 已经发生条件下的发生概率,表示为 P(A|B),读作“在 B 发生的条件下 A 发生的概率”。比如原因 A 的条件下,患有“贝叶死”的概率,就是条件概率。
- 联合概率:多个事件同时发生的概率。
- 联合分布:多个事件发生多个结果的概率分布情况。
- 似然函数:你可以把概率模型的训练过程理解为求参数估计的过程。举个例子,如果一个硬币在 10 次抛落中正面均朝上。那么你肯定在想,这个硬币是均匀的可能性是多少?这里硬币均匀就是个参数,似然函数就是用来衡量这个模型的参数。似然在这里就是可能性的意思,它是关于统计参数的函数。
贝叶斯公式
一般的二元贝叶斯公式如下:
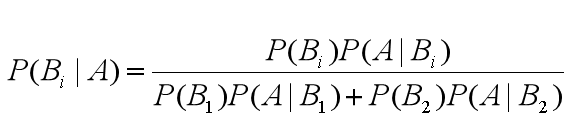
由此,我们可以得出通用的贝叶斯公式:
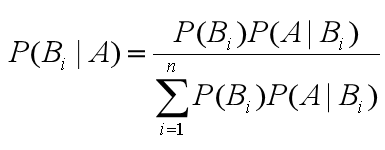
其实贝叶斯原理的可以通过条件概率公式来推理得到。
$P(Y|X)P(X)=P(X|Y)P(Y)=P(XY)P(Y|X)P(X)=P(X|Y)P(Y)=P(XY)$
放在实例中来观察贝叶斯公式的简单应用。在医疗诊断中,如果医生知道某一疾病发生某些症状的概率,那么可以利用贝叶斯公式估计得知当病人发生某症状时,推测病人发生某病的概率。
贝叶斯公式其实是反映了原因和结果之间的概率关系。
朴素贝叶斯算法
朴素贝叶斯算法是一种简单但极为强大的预测建模算法。之所以称为朴素贝叶斯,是因为它假设每一个输入变量之间是独立的。
朴素贝叶斯模型由两种类型的概率组成:
- 每个类别的概率$P(C_j)$;
- 每个属性的条件概率$P(Ai|C_j)$。
朴素贝叶斯的公式如下:
$P(Cause,Effect_1,Effect_2,Effect_3….Effect_n)=P(Cause)∏_nP(Effect_i|Cause)$
为了训练朴素贝叶斯模型,我们需要先给出训练数据,以及这些数据对应的分类。那么上面这两个概率,也就是类别概率和条件概率。他们都可以从给出的训练数据中计算出来。一旦计算出来,概率模型就可以使用贝叶斯原理对新数据进行预测。
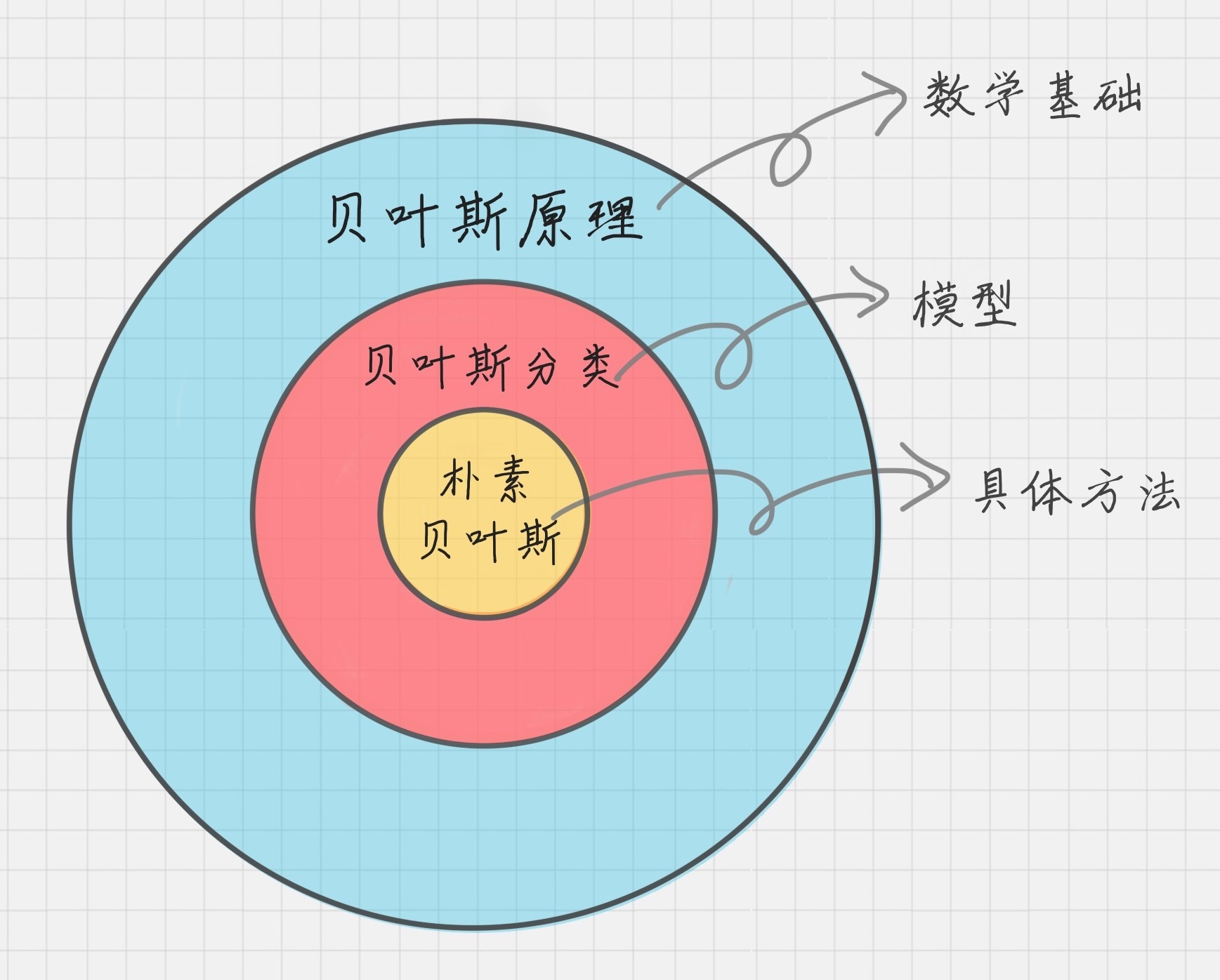
贝叶斯原理 贝叶斯分类 朴素贝叶斯之间的区别
贝叶斯原理是最大的概念,它解决了概率论中“逆向概率”的问题,在这个理论基础上,人们设计出了贝叶斯分类器,朴素贝叶斯分类是贝叶斯分类器中的一种,也是最简单,最常用的分类器。朴素贝叶斯之所以朴素是因为它假设属性是相互独立的,因此对实际情况有所约束,如果属性之间存在关联,分类准确率会降低。不过好在对于大部分情况下,朴素贝叶斯的分类效果都不错。
朴素贝叶斯分类器工作流程
朴素贝叶斯分类常用于文本分类,尤其是对于英文等语言来说,分类效果很好。它常用于垃圾文本过滤、情感预测、推荐系统等。
流程可以用下图表示:
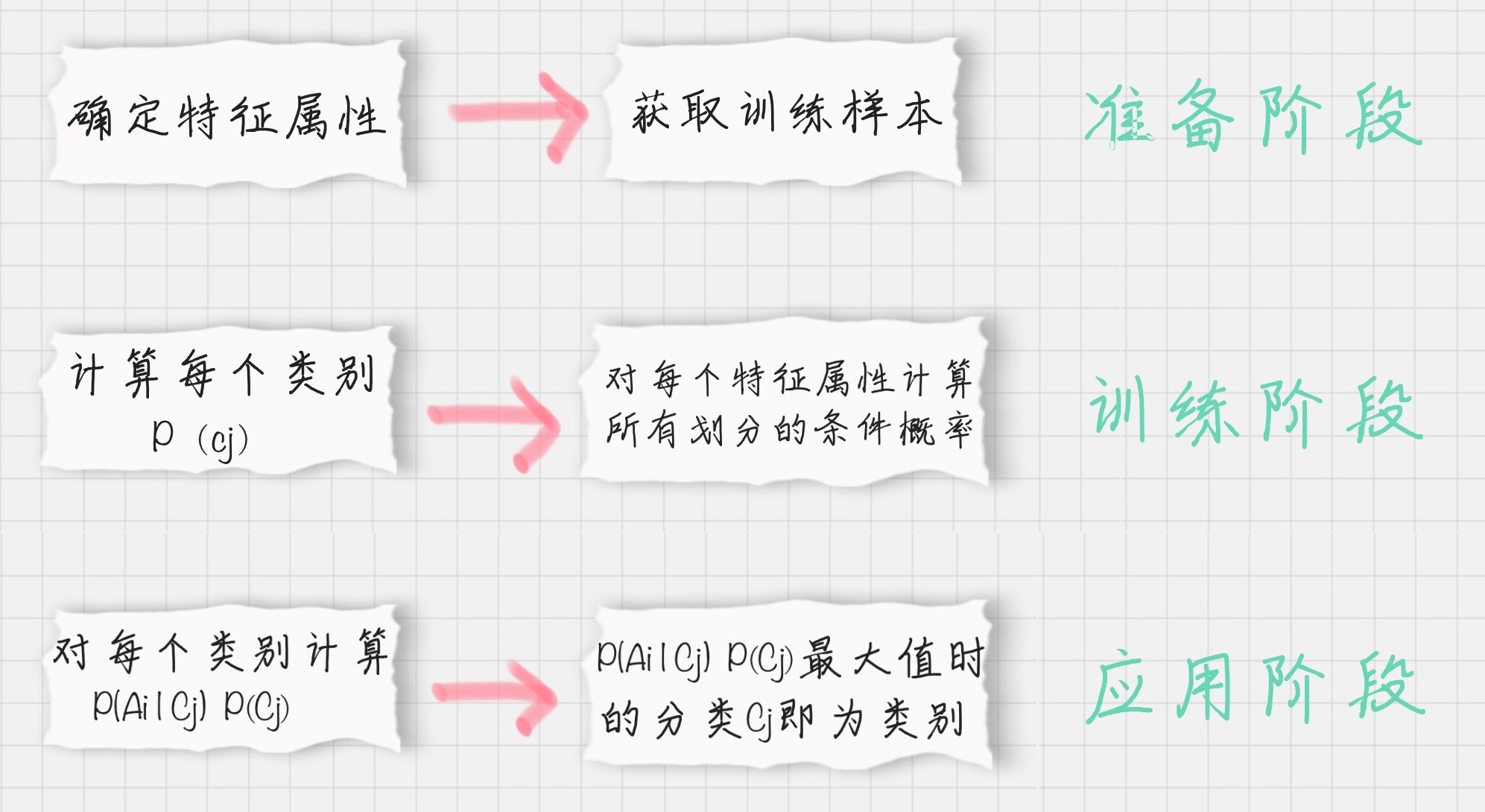
从图片你也可以看出来,朴素贝叶斯分类器需要三个流程,我来给你一一讲解下这几个流程。
第一阶段:准备阶段
在这个阶段我们需要确定特征属性,比如上面案例中的“身高”、“体重”、“鞋码”等,并对每个特征属性进行适当划分,然后由人工对一部分数据进行分类,形成训练样本。
这一阶段是整个朴素贝叶斯分类中唯一需要人工完成的阶段,其质量对整个过程将有重要影响,分类器的质量很大程度上由特征属性、特征属性划分及训练样本质量决定。
第二阶段:训练阶段
这个阶段就是生成分类器,主要工作是计算每个类别在训练样本中的出现频率及每个特征属性划分对每个类别的条件概率。
输入是特征属性和训练样本,输出是分类器。
第三阶段:应用阶段
这个阶段是使用分类器对新数据进行分类。输入是分类器和新数据,输出是新数据的分类结果。
利用朴素贝叶斯进行文档分类
朴素贝叶斯分类最适合的场景就是文本分类、情感分析和垃圾邮件识别。其中情感分析和垃圾邮件识别都是通过文本来进行判断。从这里你能看出来,这三个场景本质上都是文本分类,这也是朴素贝叶斯最擅长的地方。所以朴素贝叶斯也常用于自然语言处理 NLP 的工具。
以下是高斯朴素贝叶斯分类器的类简单实现。
1 | class NaiveBayes: |
此外,我们直接使用 sklearn 机器学习包来帮助我们使用朴素贝叶斯分类算法。
sklearn 机器学习包
sklearn 的全称叫 Scikit-learn,它给我们提供了 3 个朴素贝叶斯分类算法,分别是高斯朴素贝叶斯(GaussianNB)、多项式朴素贝叶斯(MultinomialNB)和伯努利朴素贝叶斯(BernoulliNB)。
这三种算法适合应用在不同的场景下,我们应该根据特征变量的不同选择不同的算法:
高斯朴素贝叶斯:特征变量是连续变量,符合高斯分布,比如说人的身高,物体的长度。
多项式朴素贝叶斯:特征变量是离散变量,符合多项分布,在文档分类中特征变量体现在一个单词出现的次数,或者是单词的 TF-IDF 值等。
伯努利朴素贝叶斯:特征变量是布尔变量,符合 0/1 分布,在文档分类中特征是单词是否出现。
伯努利朴素贝叶斯是以文件为粒度,如果该单词在某文件中出现了即为 1,否则为 0。而多项式朴素贝叶斯是以单词为粒度,会计算在某个文件中的具体次数。而高斯朴素贝叶斯适合处理特征变量是连续变量,且符合正态分布(高斯分布)的情况。比如身高、体重这种自然界的现象就比较适合用高斯朴素贝叶斯来处理。而文本分类是使用多项式朴素贝叶斯或者伯努利朴素贝叶斯。
TF-IDF
TF-IDF 实际上是两个词组 Term Frequency 和 Inverse Document Frequency 的总称,两者缩写为 TF 和 IDF,分别代表了词频和逆向文档频率。
词频 TF计算了一个单词在文档中出现的次数,它认为一个单词的重要性和它在文档中出现的次数呈正比。
逆向文档频率 IDF,是指一个单词在文档中的区分度。它认为一个单词出现在的文档数越少,就越能通过这个单词把该文档和其他文档区分开。IDF 越大就代表该单词的区分度越大。
所以 TF-IDF 实际上是词频 TF 和逆向文档频率 IDF 的乘积。这样我们倾向于找到 TF 和 IDF 取值都高的单词作为区分,即这个单词在一个文档中出现的次数多,同时又很少出现在其他文档中。这样的单词适合用于分类。
首先我们看下词频 TF 和逆向文档概率 IDF 的公式。


为什么 IDF 的分母中,单词出现的文档数要加 1 呢?因为有些单词可能不会存在文档中,为了避免分母为 0,统一给单词出现的文档数都加 1。
TF-IDF=TF*IDF。
你可以看到,TF-IDF 值就是 TF 与 IDF 的乘积, 这样可以更准确地对文档进行分类。比如“我”这样的高频单词,虽然 TF 词频高,但是 IDF 值很低,整体的 TF-IDF 也不高。
我在这里举个例子。假设一个文件夹里一共有 10 篇文档,其中一篇文档有 1000 个单词,“this”这个单词出现 20 次,“bayes”出现了 5 次。“this”在所有文档中均出现过,而“bayes”只在 2 篇文档中出现过。我们来计算一下这两个词语的 TF-IDF 值。
针对“this”,计算 TF-IDF 值:
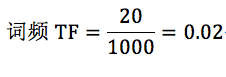
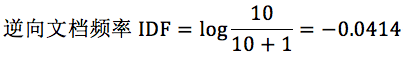
所以 TF-IDF=0.02*(-0.0414)=-8.28e-4。
针对“bayes”,计算 TF-IDF 值:
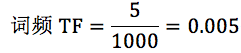
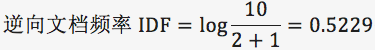
TF-IDF=0.005*0.5229=2.61e-3。
很明显“bayes”的 TF-IDF 值要大于“this”的 TF-IDF 值。这就说明用“bayes”这个单词做区分比单词“this”要好。
使用sklearn 来计算 TF-IDF
1 | from sklearn.feature_extraction.text import TfidfVectorizer |
对文档进行分类
如果我们要对文档进行分类,有两个重要的阶段:
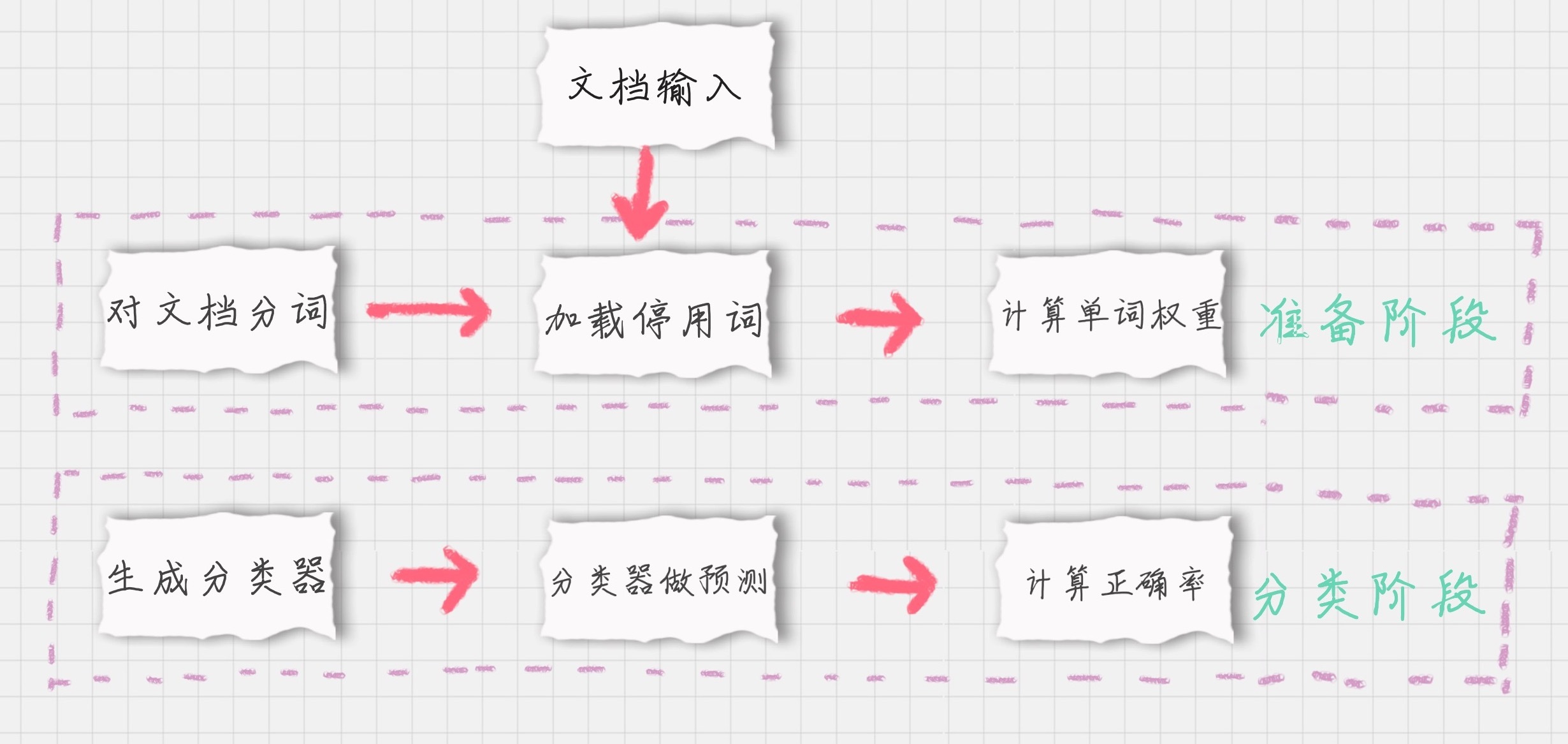
- 基于分词的数据准备,包括分词、单词权重计算、去掉停用词;
- 应用朴素贝叶斯分类进行分类,首先通过训练集得到朴素贝叶斯分类器,然后将分类器应用于测试集,并与实际结果做对比,最终得到测试集的分类准确率。
分词
在准备阶段,分词是比较重要的一个环节。在英文文档中分词的工具为NLTK包,而中文文档则是使用了 jieba包。
1 | import nltk |
1 | import jieba |
加载停用词表
我们需要自己读取停用词表文件,从网上可以找到中文常用的停用词保存在 stop_words.txt,然后利用 Python 的文件读取函数读取文件,保存在 stop_words 数组中。
1 | stop_words = [line.strip().decode('utf-8') for line in io.open('stop_words.txt').readlines()] |
计算单词的权重 TF-IDF
直接创建 TfidfVectorizer 类,然后使用 fit_transform 方法进行拟合,得到 TF-IDF 特征空间 features,你可以理解为选出来的分词就是特征。我们计算这些特征在文档上的特征向量,得到特征空间 features。
1 | tf = TfidfVectorizer(stop_words=stop_words, max_df=0.5) |
这里 max_df 参数用来描述单词在文档中的最高出现率。假设 max_df=0.5,代表一个单词在 50% 的文档中都出现过了,那么它只携带了非常少的信息,因此就不作为分词统计。
生成朴素贝叶斯分类器
我们将特征训练集的特征空间 train_features,以及训练集对应的分类 train_labels 传递给贝叶斯分类器 clf,它会自动生成一个符合特征空间和对应分类的分类器。
这里我们采用的是多项式贝叶斯分类器,其中 alpha 为平滑参数。为什么要使用平滑呢?因为如果一个单词在训练样本中没有出现,这个单词的概率就会被计算为 0。但训练集样本只是整体的抽样情况,我们不能因为一个事件没有观察到,就认为整个事件的概率为 0。为了解决这个问题,我们需要做平滑处理。
当 alpha=1 时,使用的是 Laplace 平滑。Laplace 平滑就是采用加 1 的方式,来统计没有出现过的单词的概率。这样当训练样本很大的时候,加 1 得到的概率变化可以忽略不计,也同时避免了零概率的问题。
当 0<alpha<1 时,使用的是 Lidstone 平滑。对于 Lidstone 平滑来说,alpha 越小,迭代次数越多,精度越高。我们可以设置 alpha 为 0.001。
1 | # 多项式贝叶斯分类器 |
使用生成的分类器做预测
首先我们需要得到测试集的特征矩阵。
方法是用训练集的分词创建一个 TfidfVectorizer 类,使用同样的 stop_words 和 max_df,然后用这个 TfidfVectorizer 类对测试集的内容进行 fit_transform 拟合,得到测试集的特征矩阵 test_features。
1 | test_tf = TfidfVectorizer(stop_words=stop_words, max_df=0.5, vocabulary=train_vocabulary) |
然后我们用训练好的分类器对新数据做预测。
方法是使用 predict 函数,传入测试集的特征矩阵 test_features,得到分类结果 predicted_labels。predict 函数做的工作就是求解所有后验概率并找出最大的那个。
1 | predicted_labels=clf.predict(test_features) |
计算准确率
1 | from sklearn import metrics |