以下BP神经网络推导过程是来自于NTU的李宏毅老师的ML课程。过程相当易懂,很好理解。为避免忘记,在此记录一下。视频推导链接如下(需要fq):
前导知识
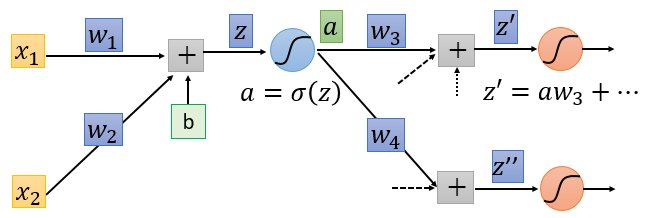
我们必须了解到的就是BP神经网络本质就是一个多层级联神经元和对应连接权重和偏置构成的函数,我们输入该函数,然后得到函数值就是模型的输出结果。
该函数具备有权重参数和偏置参数,我们需要通过输入训练数据和标签来拟合得到一组权重参数和偏置参数。拟合的方式近似于最小二乘法,我们可以得到BP神经网络的损失函数。如下:
给定训练集标签向量$O_t$和训练结果$R_t$, 我们将其训练误差$L$表示为:
$$L = \frac{1}{2} \sum_{t∈T}{(O_t - R_t)}^2 \tag{1}$$
其实也就是所有模型输出实例的预测结果减去标签真实结果的平方和的一半。我们将训练误差函数定义为一个BP神经网络模型的损失函数,我们的目标就是最小化该损失函数。求解思路看下。
求解核心思路
BP神经网络参数(权重+bias)和损失函数L($\theta$)已知,利用梯度下降法和链式法则可进行推导。
- 首先梯度下降法核心思想不变,我们需要重点关注梯度函数。

- 由于网络结构是多层的,需要使用到链式法则来求解梯度函数。

- 损失函数的微分(梯度函数)可以为关于$w_i$的多项偏微分之和。
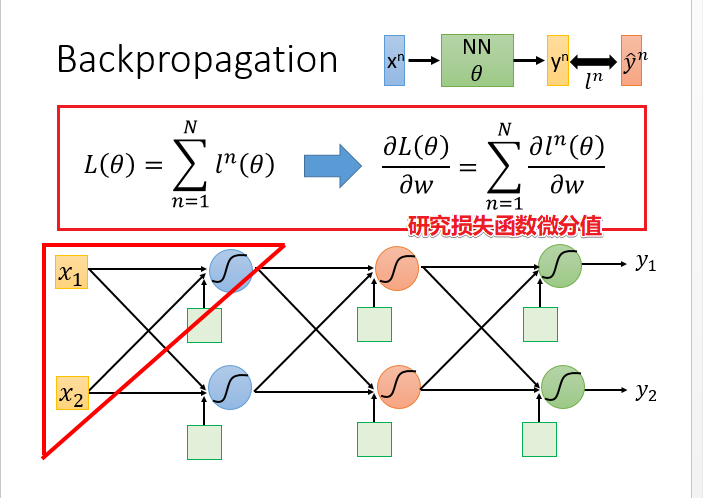
- 利用链式法则,将梯度函数差分为主要的两项(红色方框标出),然后分别进行前向和反向的迭代计算,等整个网络收敛之后,计算得到整个网络的当前梯度值,然后利用梯度下降法更新网络参数。
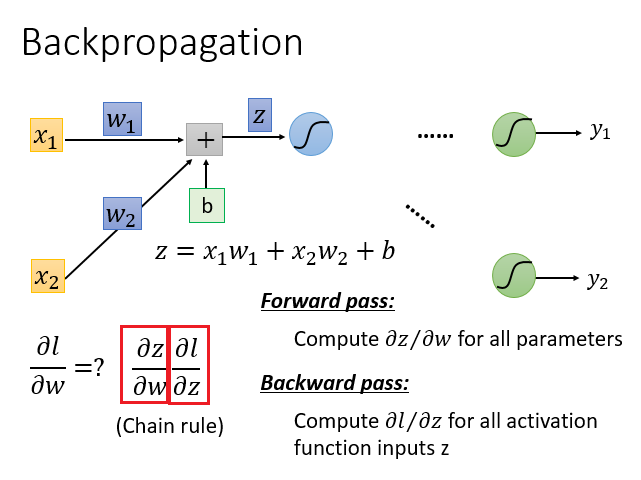
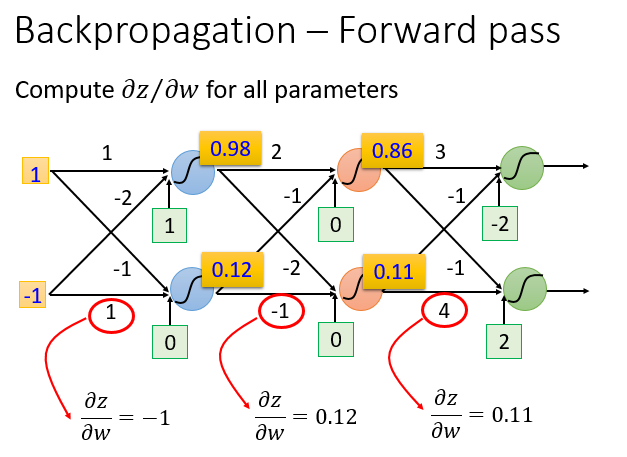
前向过程特别简单,从网络结构上来看:微分值 = 前一层的输入之和。
反向过程较为复杂,以下详细展开。
反向推导
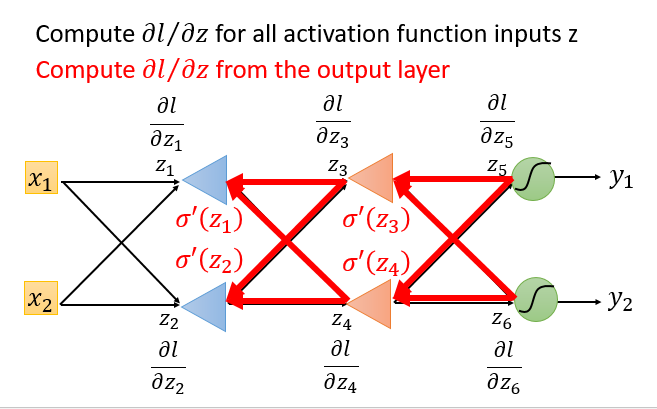
先从输入层出发考虑,可以得到一个迭代式
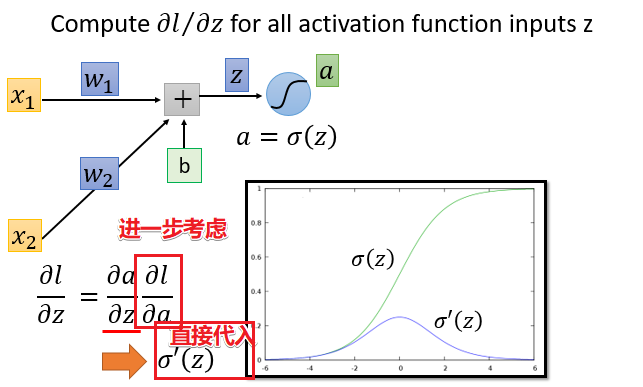
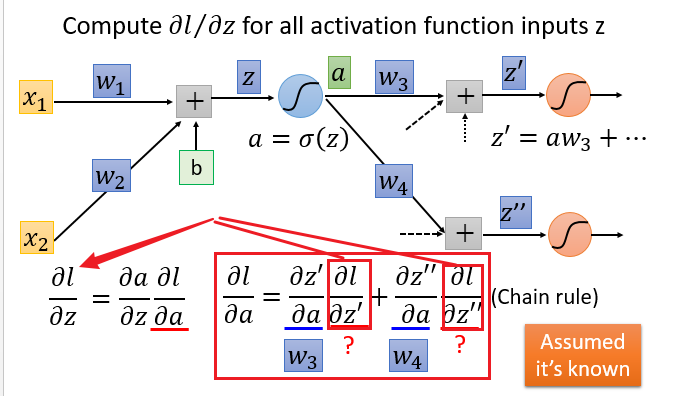
可以看出上图右边式子的小红框部分和左边式子的左边构成一个迭代关系。只不过小红框部分是下一层的微分值。从这里就可以看出来,要计算当前的微分值需要提前知道下一层的微分值,由此可以将网络结构逆转,反向进行计算。代入$w_3,w_4,\sigma’(z)$整理得到下述式子。
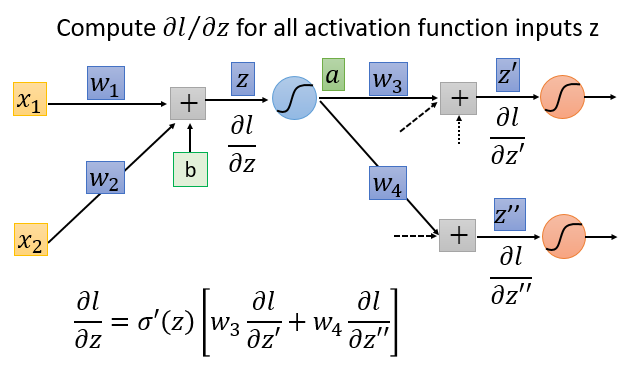
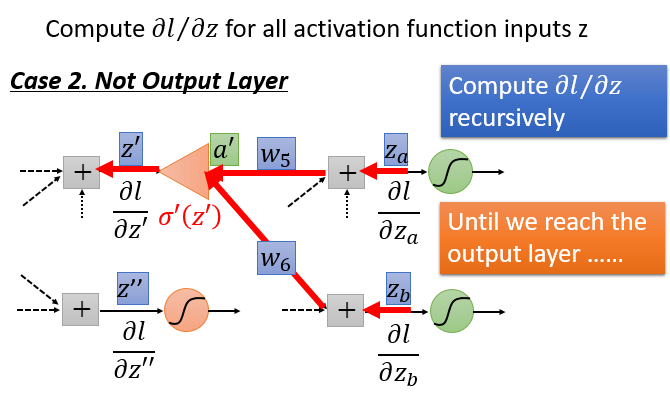
将输出层,当成输入层,激活函数为放大器。

迭代过程主要有两种情况:输出层和非输出层。
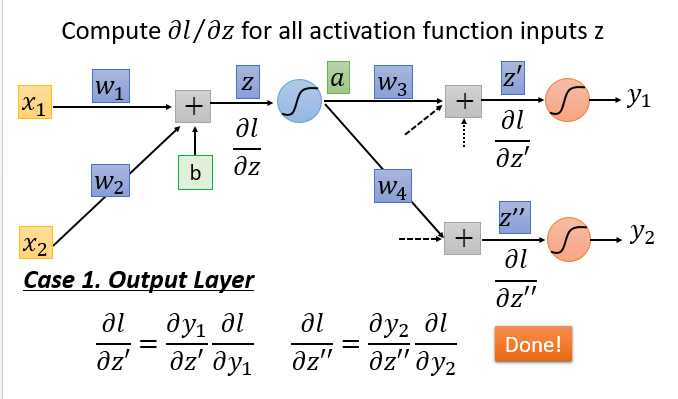
总结
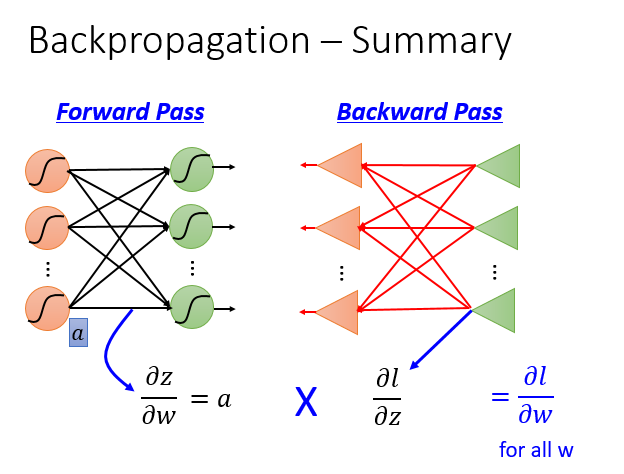
利用梯度下降法和链式法则来求解BP神经网络的损失函数的最优参数解,可分为前向和后向两个过程。前向微分是直接将当前节点的输入值求和即可。而反向微分则是需要链式法则由下一层的微分值计算得到当前层的微分值,将整个网络逆转过来,而激活函数变为普通的放大器$\sigma’(z)$。