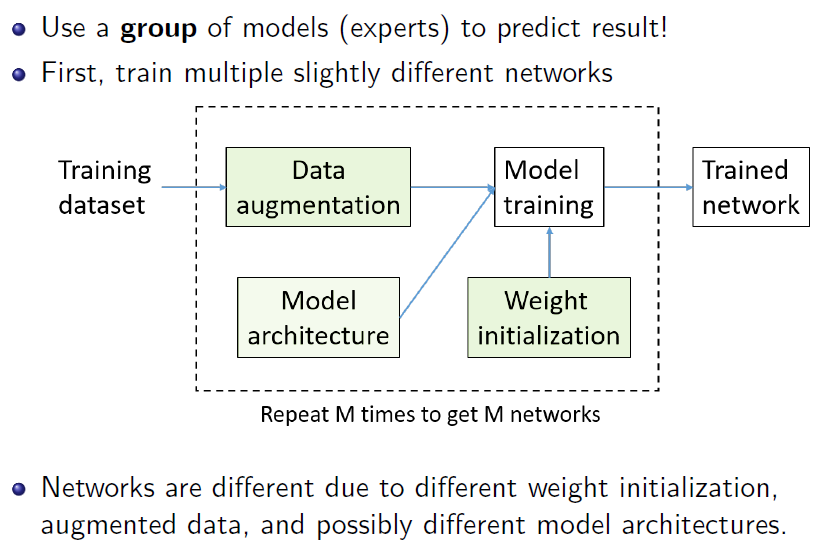
梯度爆炸和消失
在求解梯度时,通过链式法则可以使用多个中间梯度来表示初始梯度,在多层网络中,如果多个中间梯度都大于1,那么最后计算得到的梯度将远大于一,故存在梯度爆炸;
如果许多中间梯度都大于1,那么最后计算的到梯度将近乎0,故存在梯度消失。
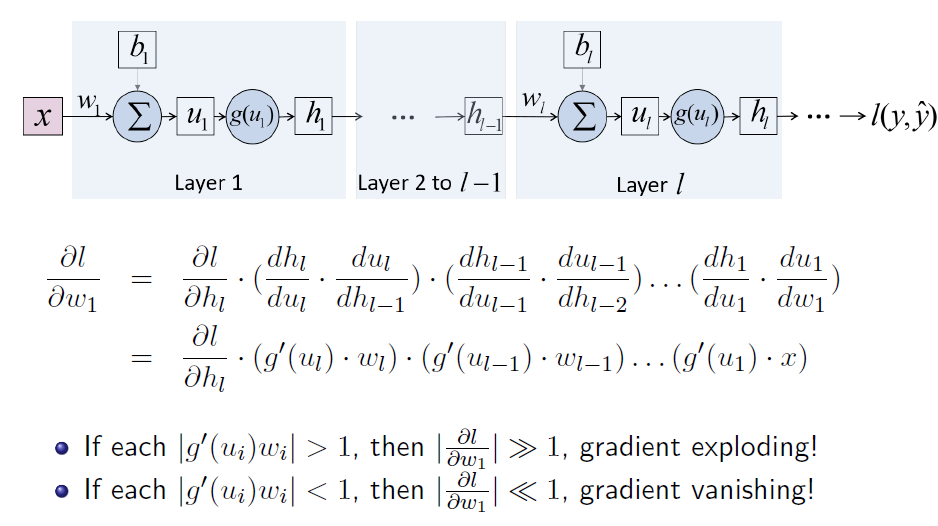
由于梯度爆炸的存在,训练过程相当不稳定。我们需要保证,激活函数的导数或权重的绝对值小于等于1。
解决梯度爆炸的策略有:
- 初始化权重值的绝对值小于1
- 在训练前对权重进行标准化
- 对输入进行归一化
梯度消失将会使训练相当慢,我们必须使激活函数倒数*权重的绝对值不要太小,解决的策略有:
- 选择ReLU激活函数
- 权重初始化,$w - N(0, \sigma^2)$
- 权重在训练前重新标准化
简单来说,在开始训练之前,网络权重初始化的策略是,从由输出维数n和m决定的正态分布或者均匀分布中采样,会加快网络的训练过程。
- 当激活函数是tanh时(Weight initialization: Xavier’s method)

- 当激活函数是ReLU时(Kaiming He 大神)

55255515524
Mini-batch 的问题
问题:每一批的数据分布不一致。
解决方法:批量归一化BN。将每一组数据都归一化为标准正态分布。(均值为0,方差为1)

BN 通常放在激活函数ReLU之前。
在合理的学习率范围内,学习率越大,BN越有效。上述的$\gamma $$,\beta$ 作为模型的参数,一并学习。
过拟合的问题
过拟合是普遍存在的,我们有以下几种策略来解决:
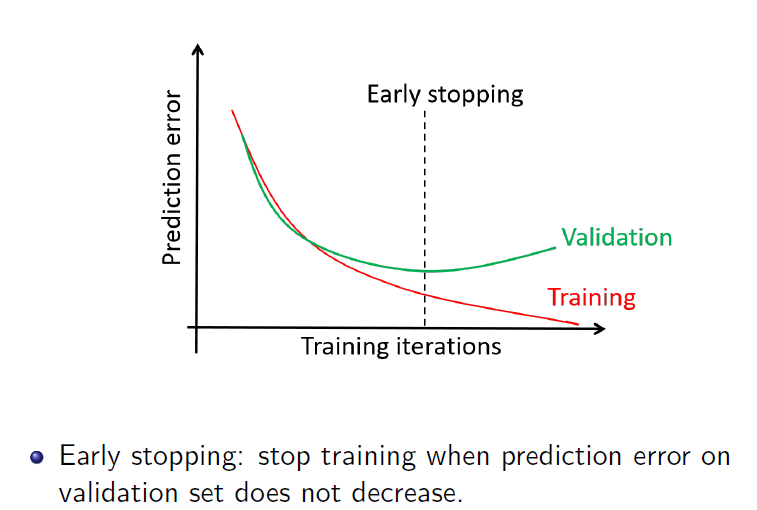
借助验证集来确定提前终止迭代的次数
正则化:$L_P$Norm

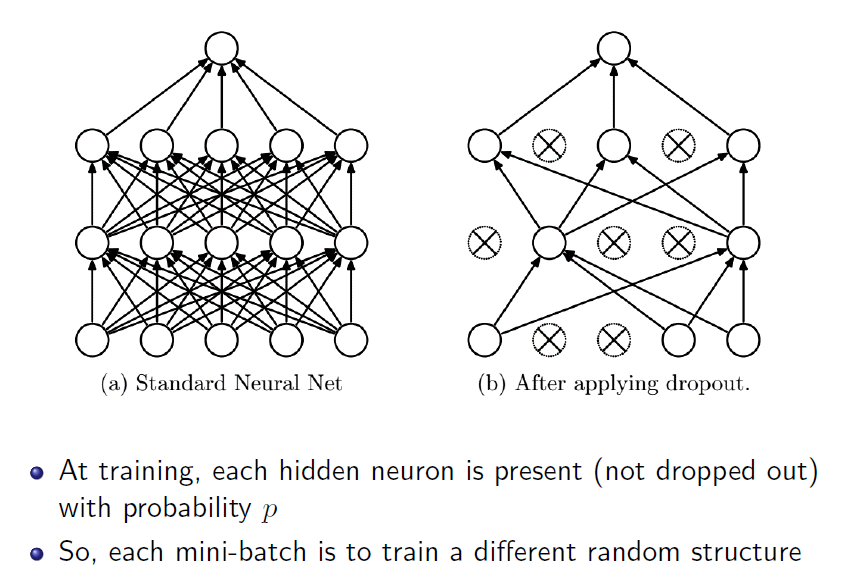
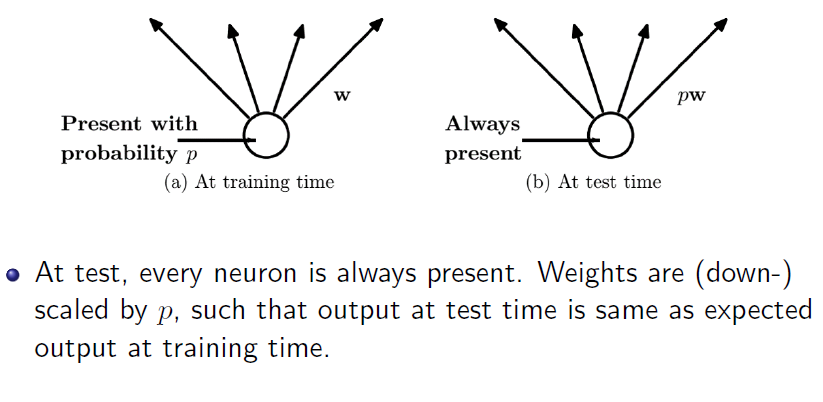
dropout
数据增广(增强)

集成模型