SVM原理

假设有两类样本，类别分别为 - 1， 1。空间中存在一个超平面能够划分这两类样本。

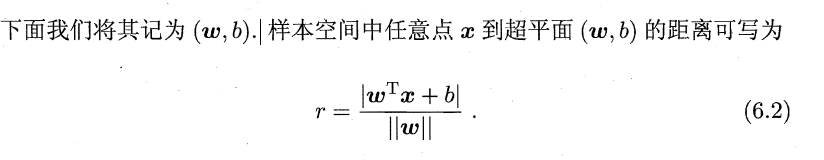
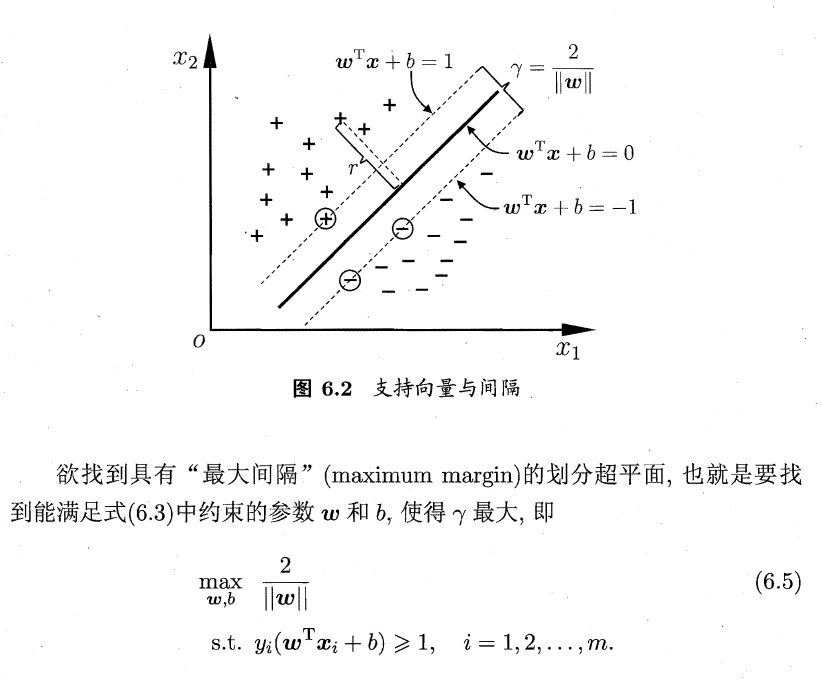
求解SVM

梳理一下过程就是：

我们记初始的目标优化函数为 f(w)。求 min f(w)。

但是这个 min f(w) 真的不太好求，所以我们引入拉格朗日乘子 a，构造了一个拉格朗日函数 L(w, b, a)。

根据KKT条件可得，当 f(w) = max L(w, b, a);

所以有 min f(w) = min max L(w, b, a)

但因为是凸规划问题，不太好求 max L，所以我们把问题转化为 min f(w) = min max L(w, b, a) >= max min L(w, b, a)。

所以我们对 w b 求偏导，令其等于0，然后代入L(w, b, a) 得到 min L(w, b, a)：

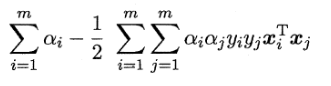
记上述式子为 g (a) = min L(w, b, a)。

于是问题转化为 min f(x) = max g(a)。

所以我们求解 max g(a)，得到 a，然后代入超平面方程得到关于 a， b的模型方程。

至于 a 我们使用 SMO算法来求解。

而位移项，我们可以通过支持向量的平均值来计算。

引入核函数的作用就是将一些低维空间的数据映射到高维空间，使之在高维空间中得以找到一个超平面进行划分，解决一些样本在低维空间的线性不可分的问题

软间隔的意思就是允许一些样本不满足到超平面的距离大于等于1的约束。

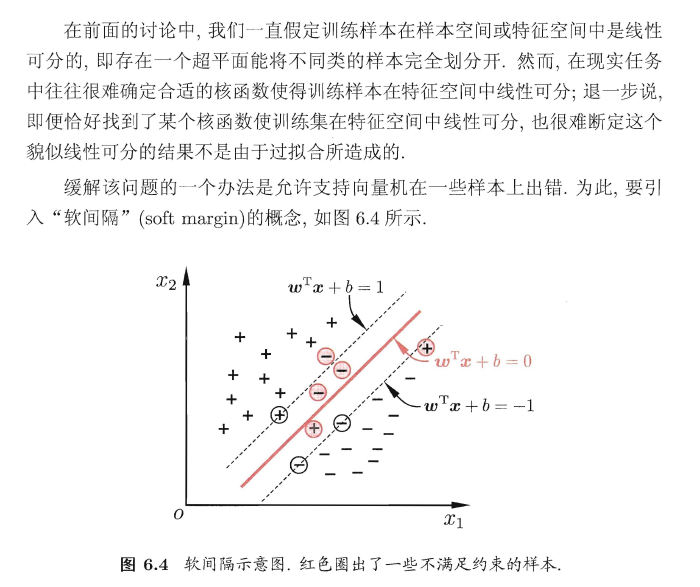
引入了软间隔，我们需要重新修改优化的目标函数。

当然我们需要保证我们最大间隔的约束性质，同时允许一些样本不受约束。建模如公式6.29.

同样的求解思路是引入拉格朗日乘子，不过这次是引入了两个乘子。

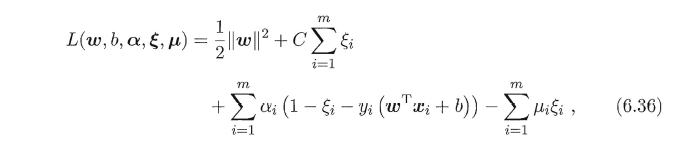
上述比较显得较为潦草，碍于个人时间有限，有些地方表达可能不太严谨，但已经大致的描述了SVM的相关概念和原理。