输出前 m 大的数

假设数组长度为 n，要输出前m大的数，m < = n，想法有两种：

  1. 先排序后输出，算法复杂度为 O(n log n)
  2. 先在 O（n）时间内将前m大的数放到数组的右边，然后对其进行快排O(mlogm)，时间复杂度为 O（n+mlogm）。

在m较小，n较大的情况下，第二种做法显然比较可取。

那么如何在 O（n）的时间内将前m大的数放在数组的右边呢。

我们引入 arrangeRight（k）：即把前K大的数放在数组的最右边。

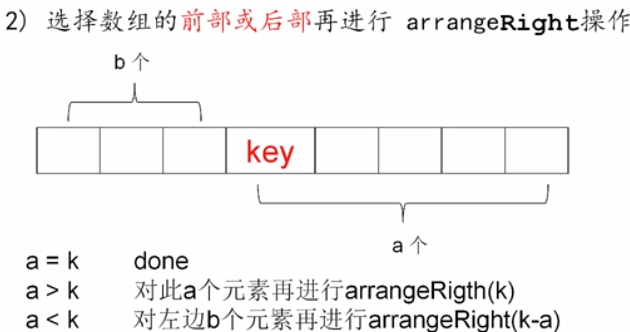
同快排一样，我们选取一个位置 a = key[0]，我们为 a 选择一个合适的位置，保证左边的数小于等于 a，右边的数大于等于a。然后判断 a右边的数组的数目和左边的数目

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
void swap(int & a, int & b){
    int tmp = a;
    a = b;
    b = a;
}

void qsort(int a[], int s, int e){
    if(s >= e){
        return;
    }
    int k = a[s];
    int i = s;
    int j = e;
    while(i != j){
        while(j > i && a[j] >= k) j--;
        swap(a[i], a[j]);
        while(i < j && a[i] <= k ) i++;
        swap(a[i], a[j]);
    }
    qsort(a, s, i - 1);
    qsort(a, i + 1, e);
}

void arrangeRight(int a[], int k, int s, int e){
    // a: 数组指针   k：前k大, s:起始索引 e:结束索引  
    int key = a[s];
    int i = s;
    int j = e;
    while(i != j){
        while(i < j && a[j] >= key) j--;
        swap(a[i], a[j]);
        while(i < j && key >= a[i]) i++;
        swap(a[i], a[j]);
    }
    if(i == e - k + 1 ) return;
    else if(i + k > e + 1) arrangeRight(a, k, i, e);
    else if(i + k < e - 1) arrangeRight(a, k-a, s, i - 1);
}

int a[6] = {1,3,4,56,7,1};
int k = 2;
arrangeRight(a, 2, 0, 5);
qsort(a, e - k + 1, e);
print...