单因子测试总结
数学模型
根据APT套利定价模型,单因子测试的含义就是, 在每一个时间截面上,也就是站在一年中的某一天关注所有股票的下一期收益率 r 和股票当期相应的因子暴露值 x 之间的关系:
$$ r = a x + b $$
也就是在某一个时间点,对每一只股票的收益率和该股票的因子暴露值做一个简单的线性回归,其中 a 为因子的收益率,b 为独立于市场的残差收益率。
《主动投资组合》书中定义:

在单因子测试报告中,提出了一种拓展。增加了行业虚拟变量和流通市值,以及相应的因子收益率。

大概思路
我们就是要利用现有的数据 股票收益率r 和 因子暴露值 x,去进行每一个时间横截面的线性回归,得到 a,b,然后利用这 a x + b = r* 求出因子预测的股票收益率。
股票收益率计算
这里得先来了解股票收益率的计算方法
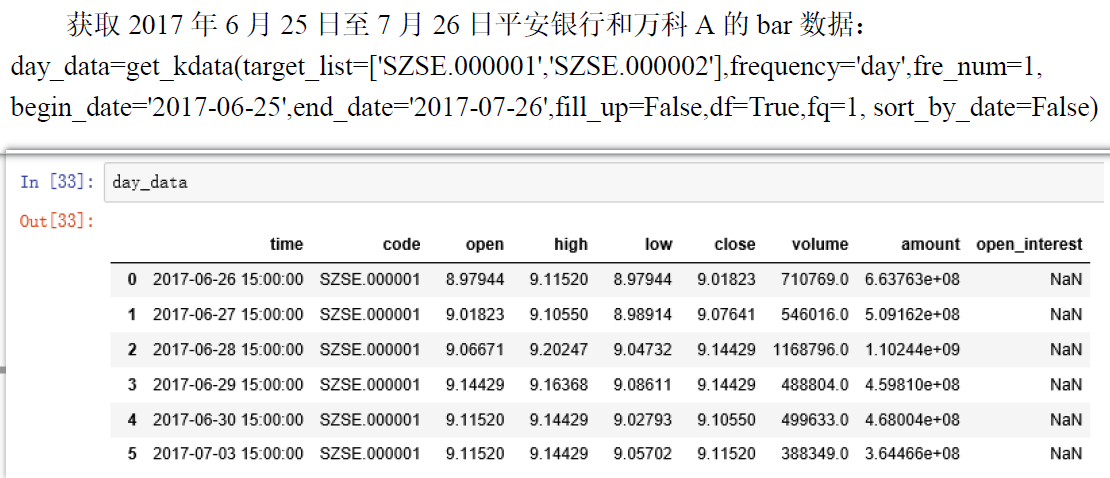
我们可以通过每一只股票的 K 线数据(get_kdata 的方式获取,如下),我们如果以1天为1期的话,那么有:
股票收益率 = 第二天股票收盘价格 / 第一天股票收盘价格 - 1 (收盘价格就是下列的 close 字段)
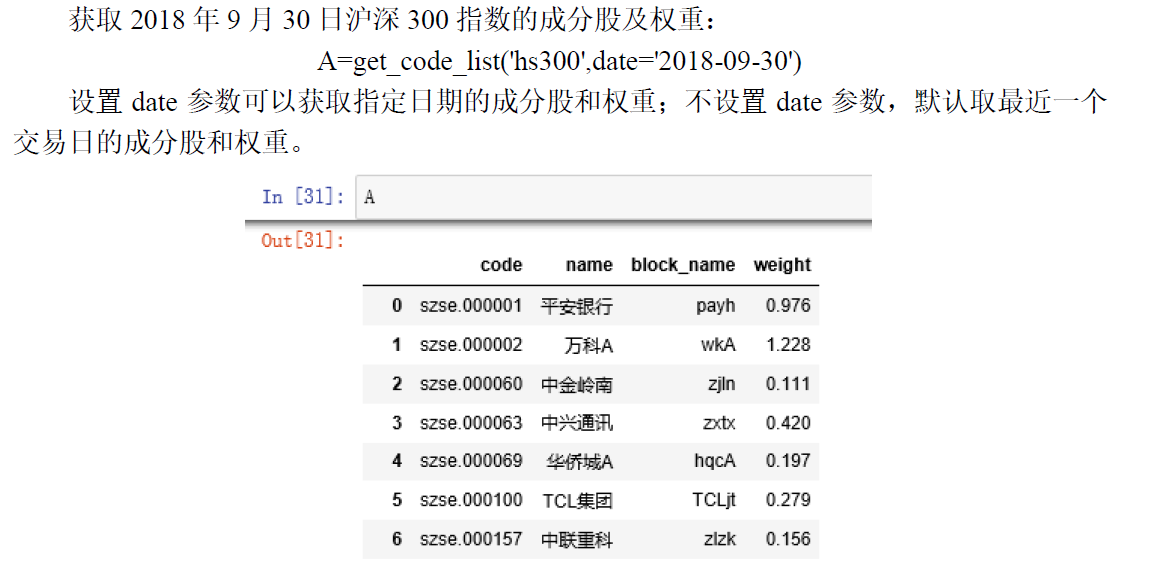
然后在每个时间截面获取每一个的股票收益率情况,利用成分股的权重,加权求和得到在该时间点上的股票市场整体收益率。
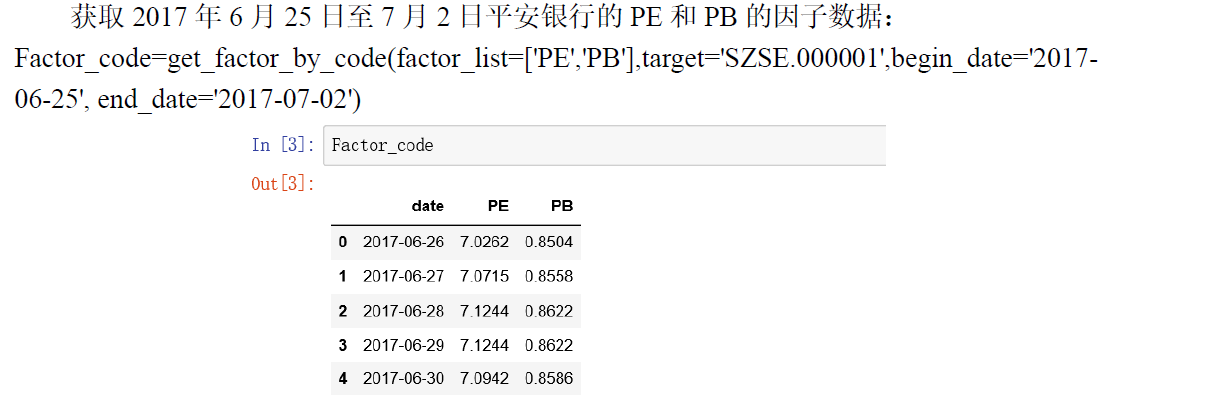
因子暴露值
每一只股票在每一时刻都有对应的因子暴露值,获取方法如下。
我们需要对因子进行预处理,一般是
- 中位数去极值法去除异常值。
- 缺失值处理,可剔除或者均值填充。
- z-score 规范化,使之标准差为 1,均值为0。

计算夏普率
到这里我们可以在每一个时间面上对所有股票的收益率和因子值进行回归,得到 因子收益率 a 和残差收益率 b。
然后重新预测所有股票的收益率。先对所有成分股的权重求和,然后每个权重除以总权重得到新的权重,使用加权求和的方式计算在该时间点的股票池中的总体收益率。
在每个时间点上重复上述计算就可以得到一个产品收益率的时间序列。然后就可以计算超额收益率序列,从而计算夏普比率。)这里的无风险收益率一般取 4 % 。

利用上述数据也可以计算 IC值,年化收益率,IR值,t 检验结果等等。
更新补充:
由于是每一个月初开始调仓(近似于买入卖出股票),那么我们就可以把每一期预测的周期视为一个月。一年划分成十二个时间截面来回归。回归的自变量是月初当天的每个股票对应的因子,因变量是这一个月内的日平均收益率或者日平均对数收益率(计算方法是月末-月初/月初股票的收盘价格)。接着拟合十二个回归模型。
接下来计算超额收益率平均值思路是:
在每一个拟合好的时间模型上,计算每只股票的收益率,然后通过个股权重,加权组合求得当月股票池的总平均收益率。然后使用这12个月的时序产品总平均收益率序列,作为产品收益率序列数据来计算夏普比率。此时 n = 12
思路主要来自于知乎文章
个人理解:emmm 不就是使用月初因子作为训练数据,平均收益率作为训练标签,使用线性回归模型进行拟合么。应该可以引入惩罚项吧?或者使用其他机器学习模型来训练??
共线性筛选
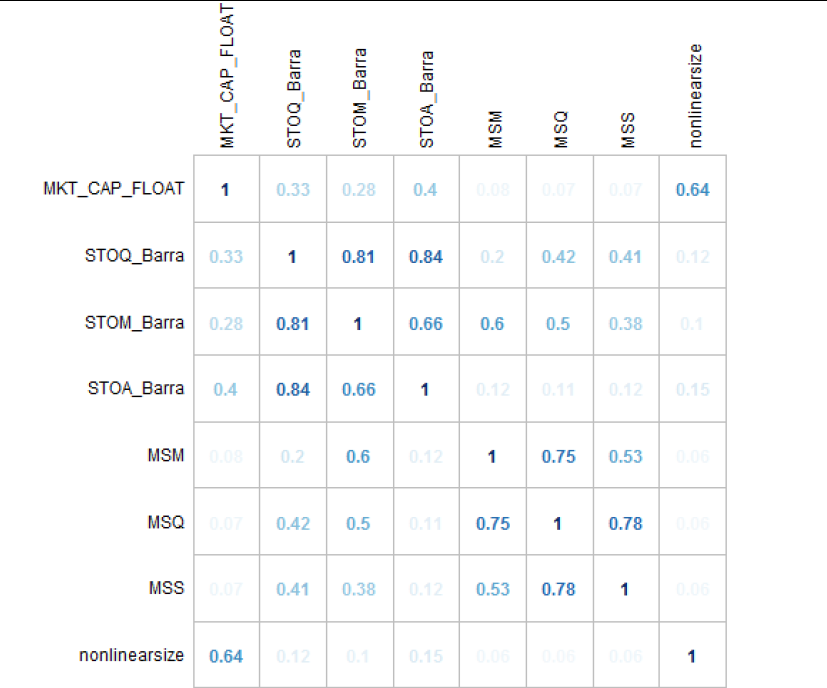
我们使用上述方法可以得到每一个因子的年化夏普率,然后挑选较优的各大类因子,得到一个列表。但此时依旧需要解决因子之间的共线性问题,如果两个因子的线性关系较为明显(相关系数为1正相关,相关系数为-1负相关),我们应该剔除,保留其中一个,或者合成新的因子。

利用相关性矩阵来计算的结果如下。
分层回测
分层就是将全体股票池按市值等分为大、中、小股票池。然后分别对每个池进行上述的测试。题目里头也有提及到不同市值的股票风格不同,所以觉得这个可能还是有点必要的。

总体过程
- 确定测试的开始和结束日期;
- 股票日频数据采集,构成股票池;(所有股票的K线时序数据)(此处可按市值进行分层)
- 利用K线数据计算所有股票的每期收益率;(收益率时序数据)
- 确定候选的测试因子集合;
- 获取股票池中每个股票的候选因子,也就是股票对因子的暴露值;(因子时序数据)
- 对每个因子进行预处理;
- 每一个时间截面(每一天)对当期的因子暴露值和股票的下期收益率进行回归,得到因子收益率和残差收益率。
- 利用回归得到的因子收益率和残差收益率和因子暴露值,计算股票的预测收益率
- 每个时间截面计算整体股票池的预测收益率,得到一个收益率序列。
- 根据收益率序列计算夏普率,筛选较好的因子。
- 使用相关性矩阵,剔除相关性较强的因子,得到最后的因子集合。