论文:Multi-objective workflow scheduling in cloud system based on cooperative multi-swarm optimization algorithm
作者:YAO Guang-shun(姚光顺) DING Yong-sheng(丁永生) HAO Kuang-rong(郝矿荣)
摘要
本算法名为多种群多目标优化算法(MSMOOA),其目的就是提高云系统中工作流调度的性能。该算法受物种划分为种群的思想启发,物种可根据不同目标划分得到不同的种群,但同时种群有具备一定的信息共享。基于此,数据中心的每一个物理机都可认为是一个种群,均采用多目标粒子群群优化算法来搜寻单一目标的非支配解。每一个种群中的粒子都可以被划分为两个类别,采用不同的策略进行协同进化。
其中一类可以与多个种群进行同步通信,提高种群间的信息共享程度,另一类粒子则负责在同一个种群内部进行交换信息。
而且,为了避免弹性可用资源的影响,本文采用了一个管理服务器来收集云数据中心中用于调度的可用资源。
本文使用混合并行的工作流应用来评估本算法,并和其他相关的方法进行对比。结果显示采用本算法有更好的性能提升。
引言
工作流技术应用于对科学和工业应用的建模。一个工作流任务通常具备许多具有优先约束的子任务。其中任务的输入输出之间具有依赖关系。
在分布式异构计算系统中,如何将工作流的任务调度到可用的计算资源中 np完全问题,是一个主要的挑战。当下学界已经提出了许多针对分布式计算系统中不同目标、不同视角下工作流调度的有效算法。
最近,云计算成为一种革命性的范式,适合于以即付即用的模式改变向客户提供异构服务和计算资源的方式。有了云计算,客户可以在瞬间扩展到巨大的容量,而无需支付软件许可证和投资新的基础设施。
云计算背景下的工作流调度难点在于要考虑多种不同的因素。第一,消费者和云服务供应商的目标不同,客户通常对最小化完工时间和应用程序的成本感兴趣,而云服务供应商通常对最大化资源利用率、最小化能源消耗或用户公平性感兴趣。
所以调度问题必须处理为一个多目标优化问题(MOOP),其目标是优化多个可能存在冲突的准则,其中不可能找到所有目标的全局最优解。此外,云数据中心通过虚拟化技术以虚拟机(VM)的形式为客户提供服务,运行的VM可以根据系统的工作负载动态伸缩。因此,调度策略应该能够在更改发生后尽快检查可用的计算资源。
当前工作的缺陷主要有:1. 通过把所有的目标集中在一个分析函数中的单目标问题。计算出的解决方案依赖于所选的权重,而这些权重通常是由先验决定的,不需要了解工作流、基础设施,通常也不需要了解要解决的问题。因此,如果权重不能准确地捕捉用户的偏好,计算出的解决方案可能不能满足所解决问题的要求。2. 其他方法基于按顺序方式对不同的目标进行排序。但是,目标的数量是有限的,目标优化的顺序需要某种优先信息,而这些信息可能很难得到。
近年来,基于帕累托的多目标任务调度方法得到了广泛的应用。主要有:1. 基于实例库和帕累托解的混合遗传算法求解最大完工时间和能耗优化问题的帕累托解;2. 基于帕累托的启发式列表调度算法,为客户提供了一套关于完工时间和能耗的折衷最优解。但是局限在于只关注两个目标。上述方法都没有集成到云数据中心的结构中,云数据中心由多个物理机器(PMs)组成,可以通过内部网在这些PMs之间共享信息,而且未能考虑云计算环境下计算资源的动态变化。
在这项工作中,我们也采取了三个目标(时间、成本和能源)。并设计了一种用于云计算工作流调度的多群多目标优化算法(MSMOOA)。
为了获得调度所需的计算资源,首先设计了一个数据中心模型。该模型采用manager服务器接收客户提交的工作流后收集可用计算资源的信息,有效地避免了弹性资源对调度结果的影响。MSMOOA利用云数据中心的结构来搜索非主导调度方案。在MSMOOA中,每个可用的PM都被看作是一个群,并采用改进的多目标粒子群优化算法(MOPSOA)来寻找一个目标的非优势解。通过PMs之间的内部网连接,一个群中的一些粒子可以从其他群中获取信息,这些粒子的速度更新也受到其他群状态的影响,促进了群之间的信息共享与协作。我们还设计了一些新的更新策略来提高粒子的搜索能力。
我们的主要贡献在于:
- 提出了一种新的多群协同机制,并对该机制中粒子速度的更新进行了修正。粒子速度的更新不仅受个体和全局最优的影响,而且受群体最优的影响。
- 提出的MSMOOA算法用于云系统中的多目标工作流调度,是第一个考虑云数据中心结构特点的工作流调度算法。
问题建模
多目标问题概念
现实世界中的大多数工程问题都是多目标优化问题。MOOP的目标是找到一组好的权衡解决方案,决策者可以根据自己的偏好从中选择一个。由于Pareto给出了多目标优化中最常见的最优定义,因此提出了许多求解MOOPs的研究工作。
由于MOOP涉及多个目标,所以对于所有目标,不存在单一的最优解决方案。应该找到在所有目标之间具有权衡或良好折衷的解决方案,通常采用帕累托最优。相关的帕累托概念如下:
帕累托支配。
帕累托最优。
帕累托最优集合。
pareto最优前沿
见Definition 1~4.

云数据中心模型
本工作中使用的云数据中心提供了云服务提供商以VM的形式提供的一组资源,该资源采用即付即用模型。在我们的模型中,云数据中心由一组PMs组成。
根据以上情景,我们可以抽象出两种对象,一个是数据中心由多个物理机组成,而一个物理机因为虚拟化技术的原因,可以建模成不同的虚拟机:
每个PM都可以通过内部网与位于同一数据中心的其他PM通信,所有这些与manager服务器连接的PM组成了云数据中心。每个PM都可以通过内部网与位于同一数据中心的其他PM通信,所有这些与manager服务器连接的PM组成了云数据中心。云数据中心通过manager服务器通过Internet向客户提供服务,manager服务器保存云数据中心中可用资源的信息,接收客户提交的工作流,并存储发现的非主导解决方案。manager 服务器接受来自客户的工作流,首先第一步将会检查VM和PM的可用信息。
该模型不允许抢占情况的发生,一旦一个任务开始就不会被中断。每一个VM一次只能执行一个任务。

云应用模型
我们使用DAG 有向无环图来表示用户工作流应用提交到云计算系统的过程。
DAG = V = (T,E)T 代表任务节点,E 代表任务控制连接和数据流关系。
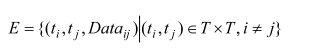
任务之间的关系有串行,并行,选择进行等关系。
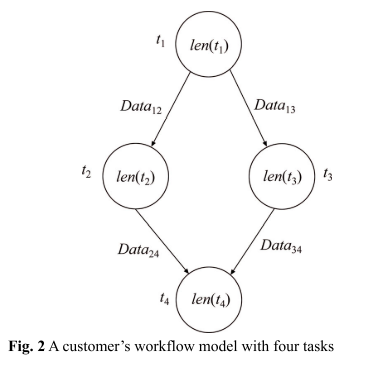
我们使用$pred(t_i)$ 和 $succ(t_i)$ 来表示当前任务的前继任务和后继任务。
而每个任务则使用$len(t_i)$ 任务的长度来表示。长度可以通过执行的指令数来度量,目的是反映该任务的执行时间和能源消耗。
调度模型
Makespan 完成时间
我们模型的第一个objective O1,是指运行在一个VM上的一个任务的完成时间,我们可以计算为最长输入传输时间的和任务计算时间的总和。

$sched(t_p)$ 代表执行任务tp的VM;
$Data_{pr}$ 是从任务 $t_p$ 传输到 任务$t_r$ 的数据大小。
$b_{sched(t_p) -> ij}$ 代表$sched(t_p)$ VM到$ij$ VM 的带宽大小。
$len(t_r)$ 代表任务$p_r$ 的长度。
$s_{ij}$ 是VM的计算速度。
如果考虑任务之间前后的关系,那么实际完成时间建模如下:

整个DAG任务的完成时间取所有任务的最长完成时间。(??为啥不是加起来。。。
经济费用
现在云服务商主要采用两种付费模式,一个是按流量付费,一个是使用时间付费,即付即用。
于是有了我们模型的第二个objective 经济费用 O2。

能源消耗
以下是第三个目标,能源消耗。

调度模型
综合以上三个目标,本文建立的多目标优化调度模型如下:
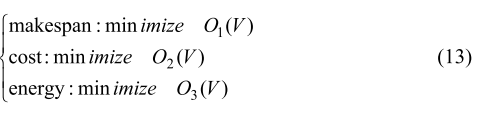
基于多种群优化算法的多目标工作流调度
粒子群优化算法PSO
在本模型中,候选的解决方法视为粒子,多个解决方法作为一个种群。

一个粒子在当前搜索空间的位置都是表示一个潜在的解,需要在不断的迭代中更新解。
在每一个迭代中,每一个粒子依据公式14,15来进行位置和速度的更新。
多群多目标优化 MSMOOA
一个数据中心包含多个物理机(多集群群),而一个物理机就包括多个VM(粒子)。然后加以上述三个约束目标。
每一个集群的粒子被分为两类:
- 该粒子群只属于一个粒子群,按照粒子群的规则发展;
- 第二类粒子群与多个群通信,并与这些群获取进化信息,这些粒子的速度和位置的更新不受群规则的影响。
每个粒子群利用单群多目标优化算法MOPSO寻找单目标非优势粒子,然后不同集群获得的所有非优势粒子协同工作,最终得到全局非优势解。
与大多数现有的MOPSO算法一样,具有最大容量的外部存档称为每个PM中的本地外部存档(LEA)和全局外部存档(GEA)
粒子表示
每个粒子都用一个由n个元素组成的向量表示(n是DAG中的任务总数),每个元素都有三个整数值,分别表示DAG中的任务数量、PM的数量和VM的数量。
这个粒子表示任务1被调度到第一个PM中的第二个VM,任务2被调度到第二个PM中的第一个VM,以此类推。
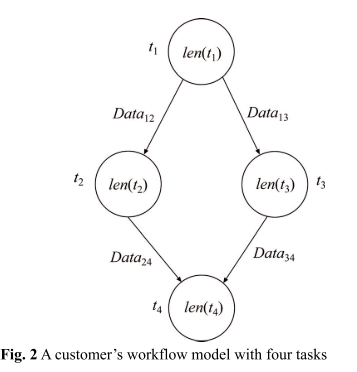

使用MSMOOA 处理工作流调度
我们的工作有三个适应度函数:1) 根据式(8)最小化最大完工时间O1(V),根据式(10)最小化经济成本O2(V),根据式(12)最小化能耗O3(V)。
由于粒子分类,第一类遵循自身种群规则的的粒子更新速度计算为:(svi第i个粒子在第s个粒子群中的速度)
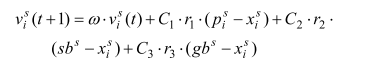
就像一些个体可以与自然界中的其他群体交流一样,MSMOOA中的另一类粒子也可以在其他群体中迁移,并从这些群体中获得信息。其速度更新为:
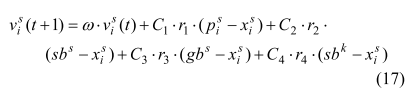
但是粒子的的位置更新一样。

- 更新一个粒子的最佳position best。如果当前值与先前位置不能相互支配,则选择该群体目标值最小的位置作为新的pbest。

- 更新LEA和sbest(最优解),通过三种适应度函数对群体和LEA中的所有粒子进行评估,并通过基于帕累托优势的物种技术将非优势解加入到LEA中。如果LEA不是满的,所有非支配解都保存在LEA中。
更新机制:

为第二类粒子更新osbest。第二类粒子可以通过内部网与不同的群通信,获得这些群的sbest。对于第二类中的每个粒子,如果其中一个粒子优于其他粒子,则选择它为osbest。否则,选择粒子所属群体目标值最小的sbest作为osbest
新GEA和gbest的所有粒子。GEA是MSMOOA的输出,由所有LEAs的解组成。在更新所有LEAs之后,将这些LEAs中的解决方案添加到GEA中,并删除主导解决方案。如果归档文件的大小超过GEA的最大容量,则根据元素的密度进行截断,以保持输出的高性能。采用拥挤距离[35]估计各单元的密度。拥挤距离值越大,表示解越好。
GEA中的所有解首先根据不同目标的适应度进行多队列排序。


