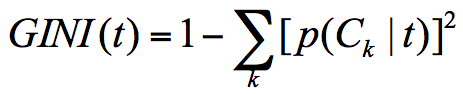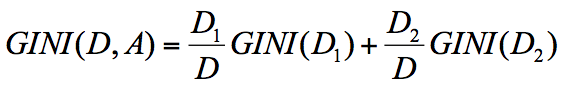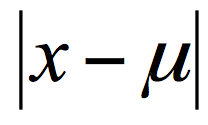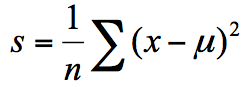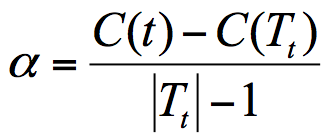决策树的工作原理

定义

决策树就是根据已有的规则条件进行评判，给出决策结果。

一棵决策树一般包括根结点，内部结点，和叶节点。根结点是一开始的判断条件，内部结点是中间过程的判断条件，而叶结点则对应着决策结果。

使用决策树时一般会经历两个阶段：构造和剪枝。

构造

决策树的构造过程就是选择什么样的属性作为决策结点的过程。我们需要经过计算合理构造节点之间的关系。

在构造过程中，要解决三个重要的问题：

  1. 选择哪个属性作为根节点；

  2. 选择哪些属性作为子节点；

  3. 什么时候停止并得到目标状态，即叶节点。

    ​

剪枝

剪枝相当于给决策瘦身，避免了许多无谓的决策判断，尤其在处理大型决策树的时候，剪枝尤为必要。同时这么做，也是为了防止过拟合的现象产生。

“过拟合”指的就是模型的训练结果“太好了”，以至于在实际应用的过程中，会存在“死板”的情况，导致分类错误。

造成过拟合的原因之一就是因为训练集中样本量较小。如果决策树选择的属性过多，构造出来的决策树一定能够“完美”地把训练集中的样本分类，但是这样就会把训练集中一些数据的特点当成所有数据的特点，但这个特点不一定是全部数据的特点，这就使得这个决策树在真实的数据分类中出现错误，也就是模型的“泛化能力”差。

泛化能力指的分类器是通过训练集抽象出来的分类能力，你也可以理解是举一反三的能力。如果我们太依赖于训练集的数据，那么得到的决策树容错率就会比较低，泛化能力差。因为训练集只是全部数据的抽样，并不能体现全部数据的特点。

剪枝的方法

  1. 预剪枝（pre-pruning）
  2. 后剪枝（post-pruning)

预剪枝就是在决策树开始构造的时候就进行剪枝，方法是在构造的过程中对节点进行评估，如果对某个节点进行划分，在验证集中就不能带来准确性的提升，那么对该节点就没有必要进行划分，此时就将当前节点视为叶节点。

后剪枝就是在生成决策树之后再进行剪枝，通常会从决策树的叶节点开始，逐层向上对每个节点进行评估。如果剪掉这个节点子树，与保留该节点子树在分类准确性上差别不大，或者剪掉该节点子树，能在验证集中带来准确性的提升，那么就可以把该节点子树进行剪枝。方法是：用这个节点子树的叶子节点来替代该节点，类标记为这个节点子树中最频繁的那个类。

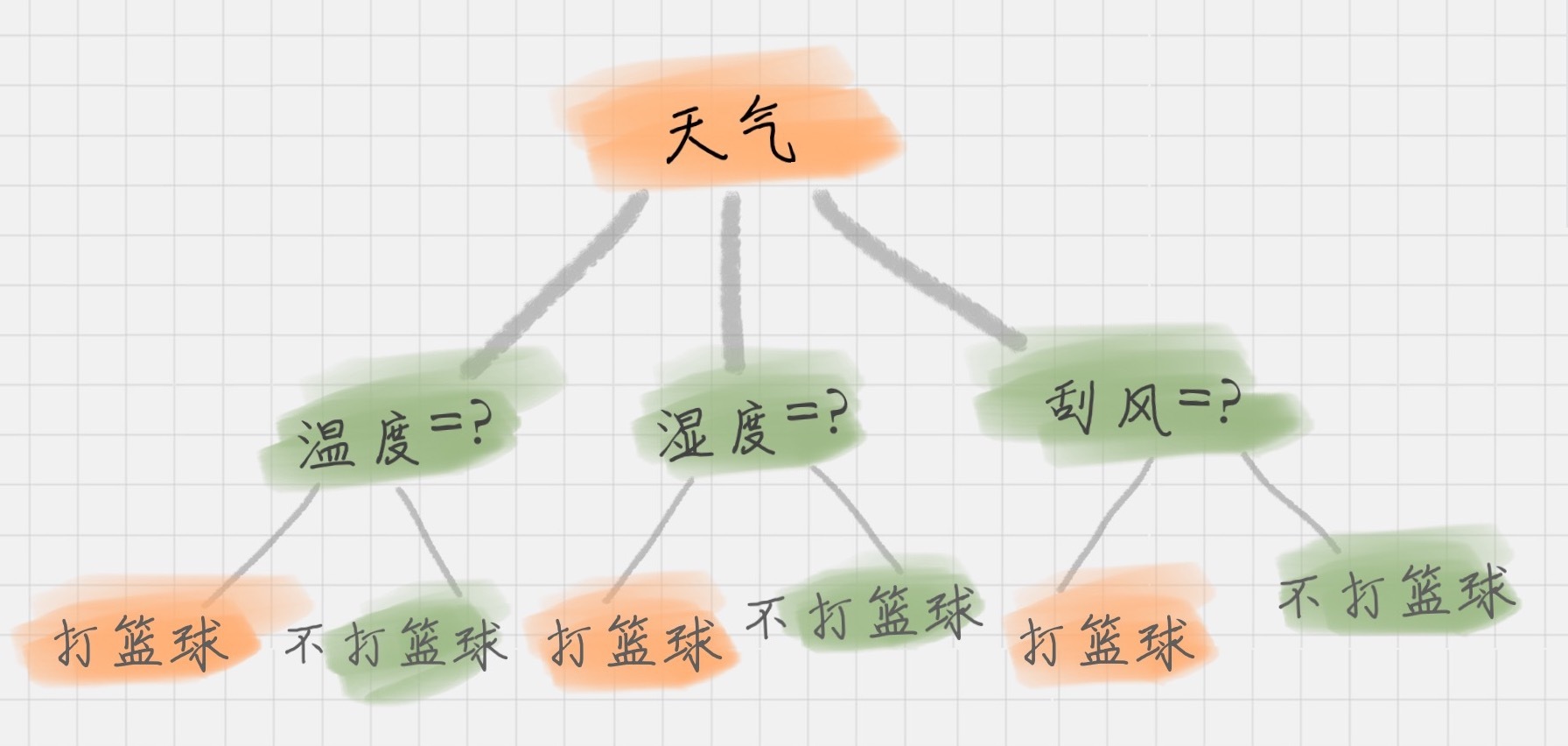
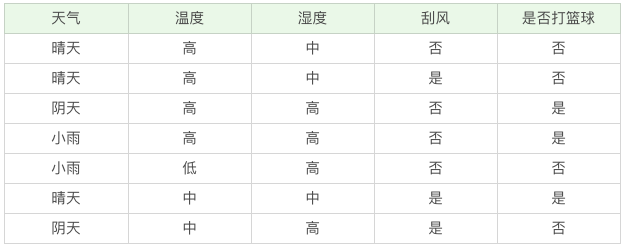
决策树构造指标

如何构造一个根据天气情况来判断是否去打篮球的决策树？以下是一个简单的数据集。

接下来进行简单的构造，我们必须思考以下问题：

  1. 哪个属性划分效果做好，作为根节点？
  2. 哪些属性作为后继节点？
  3. 什么时候停止划分，得到叶节点？

我们使用信息熵（entropy）来作为划分的指标，它表示了信息的不确定性。我们假设随机变量 $I$ 具有值 $i$，$i$ 的概率为$p_i$。

信息熵的数学公式如下：$H(x) = - \sum_{i =1}^{n} p_i log_2p_i$

同样还有其他信息指标：

  • conditional entropy（条件熵）: $H(X|Y)=\sum{P(X|Y)}\log_2{P(X|Y)}$

  • information gain（信息增益） : $g(D, A)=H(D)-H(D|A)$

  • information gain ratio（信息增益比）: $g_R(D, A) = \frac{g(D,A)}{H(A)}$

  • gini index（基尼指数）:$Gini(D)=\sum_{k=1}^{K}p_k\log{p_k}=1-\sum_{k=1}^{K}p_k^2$

信息增益越大越好，分类更正确

信息增益越大，信息给你带来的混乱程度越小。

信息论中熵越大，混乱程度越大，信息量越小，信息增益更小。

故信息增益越大的特征，在决策树上的越高。

存在多种决策树：

  • ID3 决策树 （基于信息增益划分）
  • C4.5 决策树（基于信息增益比）
  • CART 决策树 （基尼指数 ）

ID3算法简单，但解释性强，但存在缺陷，有些属性对分类任务没有太大作用，但是依旧有可能被选为最优属性。

在针对ID3算法，做了改进，于是又了C4.5算法。在 C4.5 中，会在决策树构造之后采用悲观剪枝（PEP），这样可以提升决策树的泛化能力。

悲观剪枝是后剪枝技术中的一种，通过递归估算每个内部节点的分类错误率，比较剪枝前后这个节点的分类错误率来决定是否对其进行剪枝。这种剪枝方法不再需要一个单独的测试数据集。

C4.5 可以处理连续属性的情况，对连续的属性进行离散化的处理。比如打篮球存在的“湿度”属性，不按照“高、中”划分，而是按照湿度值进行计算，那么湿度取什么值都有可能。该怎么选择这个阈值呢，C4.5 选择具有最高信息增益的划分所对应的阈值。

C4.5 在 ID3 的基础上，用信息增益率代替了信息增益，解决了噪声敏感的问题，并且可以对构造树进行剪枝、处理连续数值以及数值缺失等情况，但是由于 C4.5 需要对数据集进行多次扫描，算法效率相对较低。

决策树构造代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
# 定义节点类 二叉树
class Node:
    def __init__(self, root=True, label=None, feature_name=None, feature=None):
        self.root = root
        self.label = label
        self.feature_name = feature_name
        self.feature = feature
        self.tree = {}
        self.result = {'label:': self.label, 'feature': self.feature, 'tree': self.tree}

    def __repr__(self):
        return '{}'.format(self.result)

    def add_node(self, val, node):
        self.tree[val] = node

    def predict(self, features):
        if self.root is True:
            return self.label
        return self.tree[features[self.feature]].predict(features)
    
class DTree:
    def __init__(self, epsilon=0.1):
        self.epsilon = epsilon
        self._tree = {}

    # 熵
    @staticmethod
    def calc_ent(datasets):
        data_length = len(datasets)
        label_count = {}
        for i in range(data_length):
            label = datasets[i][-1]
            if label not in label_count:
                label_count[label] = 0
            label_count[label] += 1
        ent = -sum([(p/data_length)*log(p/data_length, 2) for p in label_count.values()])
        return ent

    # 经验条件熵
    def cond_ent(self, datasets, axis=0):
        data_length = len(datasets)
        feature_sets = {}
        for i in range(data_length):
            feature = datasets[i][axis]
            if feature not in feature_sets:
                feature_sets[feature] = []
            feature_sets[feature].append(datasets[i])
        cond_ent = sum([(len(p)/data_length)*self.calc_ent(p) for p in feature_sets.values()])
        return cond_ent

    # 信息增益
    @staticmethod
    def info_gain(ent, cond_ent):
        return ent - cond_ent

    def info_gain_train(self, datasets):
        count = len(datasets[0]) - 1
        ent = self.calc_ent(datasets)
        best_feature = []
        for c in range(count):
            c_info_gain = self.info_gain(ent, self.cond_ent(datasets, axis=c))
            best_feature.append((c, c_info_gain))
        # 比较大小
        best_ = max(best_feature, key=lambda x: x[-1])
        return best_

    def train(self, train_data):
        """
        input:数据集D(DataFrame格式)，特征集A，阈值eta
        output:决策树T
        """
        _, y_train, features = train_data.iloc[:, :-1], train_data.iloc[:, -1], train_data.columns[:-1]
        # 1,若D中实例属于同一类Ck，则T为单节点树，并将类Ck作为结点的类标记，返回T
        if len(y_train.value_counts()) == 1:
            return Node(root=True,
                        label=y_train.iloc[0])

        # 2, 若A为空，则T为单节点树，将D中实例树最大的类Ck作为该节点的类标记，返回T
        if len(features) == 0:
            return Node(root=True, label=y_train.value_counts().sort_values(ascending=False).index[0])

        # 3,计算最大信息增益 同5.1,Ag为信息增益最大的特征
        max_feature, max_info_gain = self.info_gain_train(np.array(train_data))
        max_feature_name = features[max_feature]

        # 4,Ag的信息增益小于阈值eta,则置T为单节点树，并将D中是实例数最大的类Ck作为该节点的类标记，返回T
        if max_info_gain < self.epsilon:
            return Node(root=True, label=y_train.value_counts().sort_values(ascending=False).index[0])

        # 5,构建Ag子集
        node_tree = Node(root=False, feature_name=max_feature_name, feature=max_feature)

        feature_list = train_data[max_feature_name].value_counts().index
        for f in feature_list:
            sub_train_df = train_data.loc[train_data[max_feature_name] == f].drop([max_feature_name], axis=1)

            # 6, 递归生成树
            sub_tree = self.train(sub_train_df)
            node_tree.add_node(f, sub_tree)

        # pprint.pprint(node_tree.tree)
        return node_tree

    def fit(self, train_data):
        self._tree = self.train(train_data)
        return self._tree

    def predict(self, X_test):
        return self._tree.predict(X_test)

    
datasets, labels = create_data()
data_df = pd.DataFrame(datasets, columns=labels)
dt = DTree()
tree = dt.fit(data_df)

CART算法

我们使用CART算法来生成一个分类回归决策树。ID3 和 C4.5算法可以生成多叉树，但是CART只支持二叉树。

分类树可以处理离散数据，也就是数据种类有限的数据，它输出的是样本的类别，而回归树可以对连续型的数值进行预测，也就是数据在某个区间内都有取值的可能，它输出的是一个数值。

我们使用基尼系数 来对样本进行划分。基尼系数越小，越稳定。

假设 t 为节点，那么该节点的 GINI 系数的计算公式为：

img
img

这里 p(Ck|t) 表示节点 t 属于类别 Ck 的概率，节点 t 的基尼系数为 1 减去各类别 Ck 概率平方和。

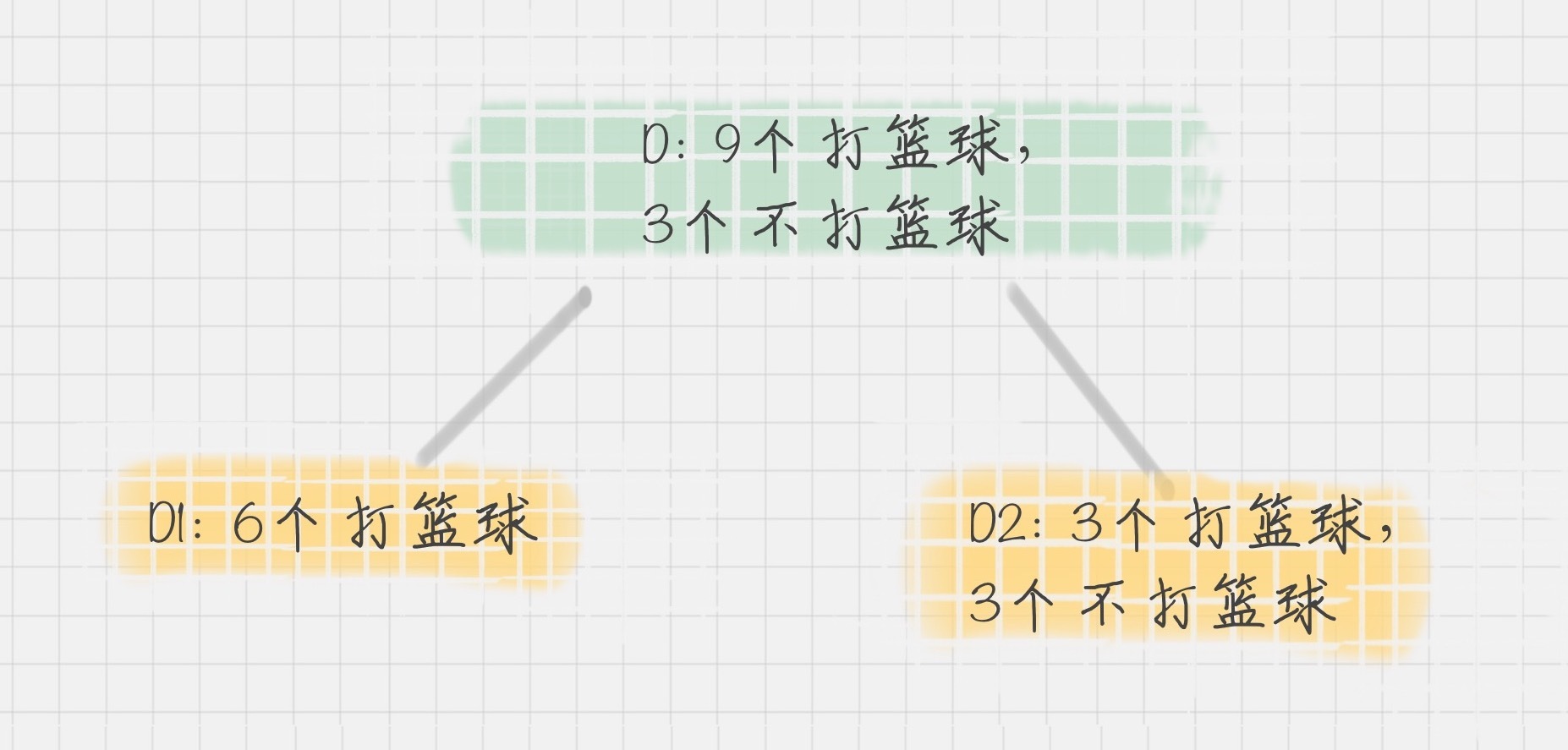
通过下面这个例子，我们计算一下两个集合的基尼系数分别为多少：

集合 1：6 个都去打篮球；

集合 2：3 个去打篮球，3 个不去打篮球。

针对集合 1，所有人都去打篮球，所以 p(Ck|t)=1，因此 GINI(t)=1-1=0。

针对集合 2，有一半人去打篮球，而另一半不去打篮球，所以，p(C1|t)=0.5，p(C2|t)=0.5，GINI(t)=1-（0.50.5+0.50.5）=0.5。

通过两个基尼系数你可以看出，集合 1 的基尼系数最小，也证明样本最稳定，而集合 2 的样本不稳定性更大。

在 CART 算法中，基于基尼系数对特征属性进行二元分裂。

假设属性 A 将节点 D 划分成了 D1 和 D2，如下图所示：

img
img

节点 D 的基尼系数等于子节点 D1 和 D2 的归一化基尼系数之和，用公式表示为：

img
img

归一化基尼系数代表的是每个子节点的基尼系数乘以该节点占整体父亲节点 D 中的比例。

分类决策树

我们使用python中的 sklearn库来完成CART分类决策树。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# encoding=utf-8
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from sklearn.tree import DecisionTreeClassifier
from sklearn.datasets import load_iris
# 准备数据集
iris=load_iris()
# 获取特征集和分类标识
features = iris.data
labels = iris.target
# 随机抽取 33% 的数据作为测试集，其余为训练集
train_features, test_features, train_labels, test_labels = train_test_split(features, labels, test_size=0.33, random_state=0)
# 创建 CART 分类树
clf = DecisionTreeClassifier(criterion='gini')
# 拟合构造 CART 分类树
clf = clf.fit(train_features, train_labels)
# 用 CART 分类树做预测
test_predict = clf.predict(test_features)
# 预测结果与测试集结果作比对
score = accuracy_score(test_labels, test_predict)
print("CART 分类树准确率 %.4lf" % score)

回归决策树

CART 回归树划分数据集的过程和分类树的过程是一样的，只是回归树得到的预测结果是连续值，而且评判“不纯度”的指标不同。在 CART 分类树中采用的是基尼系数作为标准，那么在 CART 回归树中，如何评价“不纯度”呢？实际上我们要根据样本的混乱程度，也就是样本的离散程度来评价“不纯度”。

样本的离散程度具体的计算方式是，先计算所有样本的均值，然后计算每个样本值到均值的差值。我们假设 x 为样本的个体，均值为 u。为了统计样本的离散程度，我们可以取差值的绝对值，或者方差。

其中差值的绝对值为样本值减去样本均值的绝对值：

img
img

方差为每个样本值减去样本均值的平方和除以样本个数：

img
img

所以这两种节点划分的标准，分别对应着两种目标函数最优化的标准，即用最小绝对偏差（LAD），或者使用最小二乘偏差（LSD）。这两种方式都可以让我们找到节点划分的方法，通常使用最小二乘偏差的情况更常见一些。

我们可以通过一个例子来看下如何创建一棵 CART 回归树来做预测。

这里我们使用到 sklearn 自带的波士顿房价数据集，该数据集给出了影响房价的一些指标，比如犯罪率，房产税等，最后给出了房价。

根据这些指标，我们使用 CART 回归树对波士顿房价进行预测，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# encoding=utf-8
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_boston
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
from sklearn.tree import DecisionTreeRegressor
# 准备数据集
boston=load_boston()
# 探索数据
print(boston.feature_names)
# 获取特征集和房价
features = boston.data
prices = boston.target
# 随机抽取 33% 的数据作为测试集，其余为训练集
train_features, test_features, train_price, test_price = train_test_split(features, prices, test_size=0.33)
# 创建 CART 回归树
dtr=DecisionTreeRegressor()
# 拟合构造 CART 回归树
dtr.fit(train_features, train_price)
# 预测测试集中的房价
predict_price = dtr.predict(test_features)
# 测试集的结果评价
print('回归树二乘偏差均值:', mean_squared_error(test_price, predict_price))
print('回归树绝对值偏差均值:', mean_absolute_error(test_price, predict_price))

CART 决策树的剪枝

CART 决策树的剪枝主要采用的是 CCP 方法，它是一种后剪枝的方法，英文全称叫做 cost-complexity prune，中文叫做代价复杂度。这种剪枝方式用到一个指标叫做节点的表面误差率增益值，以此作为剪枝前后误差的定义。用公式表示则是：

img
img

其中 Tt 代表以 t 为根节点的子树，C(Tt) 表示节点 t 的子树没被裁剪时子树 Tt 的误差，C(t) 表示节点 t 的子树被剪枝后节点 t 的误差，|Tt|代子树 Tt 的叶子数，剪枝后，T 的叶子数减少了|Tt|-1。

所以节点的表面误差率增益值等于节点 t 的子树被剪枝后的误差变化除以剪掉的叶子数量。

因为我们希望剪枝前后误差最小，所以我们要寻找的就是最小α值对应的节点，把它剪掉。这时候生成了第一个子树。重复上面的过程，继续剪枝，直到最后只剩下根节点，即为最后一个子树。

得到了剪枝后的子树集合后，我们需要用验证集对所有子树的误差计算一遍。可以通过计算每个子树的基尼指数或者平方误差，取误差最小的那个树，得到我们想要的结果。